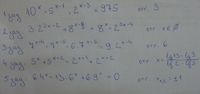
Регистрация не е нужна, освен при създаване на тема в "Задача на седмицата".
ПОКАЗАТЕЛНИ УРАВНЕНИЯ
6 мнения
• Страница 1 от 1
Re: ПОКАЗАТЕЛНИ УРАВНЕНИЯ ;( ПОМОЩ СПЕШНО Е !
1
[tex]10^x-5^{x-1}2^{x-3}=975[/tex]
[tex]10^x-5^x2^x5^{-1}2^{-3}=975[/tex]
[tex]10^x(1-\frac{1}{40})=975[/tex]
[tex]10^x.39=40.975[/tex]
[tex]10^x=40.25=1000[/tex]
[tex]x=10[/tex]
[tex]10^x-5^{x-1}2^{x-3}=975[/tex]
[tex]10^x-5^x2^x5^{-1}2^{-3}=975[/tex]
[tex]10^x(1-\frac{1}{40})=975[/tex]
[tex]10^x.39=40.975[/tex]
[tex]10^x=40.25=1000[/tex]
[tex]x=10[/tex]
- martin123456
- Математик
- Мнения: 2395
- Регистриран на: 10 Яну 2010, 18:12
- Местоположение: София
- Рейтинг: 92
Re: ПОКАЗАТЕЛНИ УРАВНЕНИЯ ;( ПОМОЩ СПЕШНО Е !
2
[tex]3.2^{3x-2}+8^{x-\frac{4}{3}}=8^x-2^{3x-4}[/tex]
[tex]\frac{3}{4}2^{3x}+2^{3x}2^{-4}=2^{3x}-2^{3x}2^{-4}[/tex]
[tex]2^{3x}(\frac{3}{4}+\frac{1}{8}-1)=0[/tex]
изразът в скобите не 0, а [tex]2^y \ne 0[/tex] => няма р корени
[tex]3.2^{3x-2}+8^{x-\frac{4}{3}}=8^x-2^{3x-4}[/tex]
[tex]\frac{3}{4}2^{3x}+2^{3x}2^{-4}=2^{3x}-2^{3x}2^{-4}[/tex]
[tex]2^{3x}(\frac{3}{4}+\frac{1}{8}-1)=0[/tex]
изразът в скобите не 0, а [tex]2^y \ne 0[/tex] => няма р корени
- martin123456
- Математик
- Мнения: 2395
- Регистриран на: 10 Яну 2010, 18:12
- Местоположение: София
- Рейтинг: 92
Re: ПОКАЗАТЕЛНИ УРАВНЕНИЯ ;( ПОМОЩ СПЕШНО Е !
3
[tex]7^{x-4}-7^{x-5}-6.7^{x-6}=9.2^{x-4}[/tex]
[tex]1-7^{-1}-6.7^{-2}=9(\frac{2}{7})^{x-4}[/tex]
[tex]x-4=log_{\frac{2}{7}}{\frac{1-7^{-1}-6.7^{-2}}{9}}[/tex], дясната страна сигурно е 2
[tex]7^{x-4}-7^{x-5}-6.7^{x-6}=9.2^{x-4}[/tex]
[tex]1-7^{-1}-6.7^{-2}=9(\frac{2}{7})^{x-4}[/tex]
[tex]x-4=log_{\frac{2}{7}}{\frac{1-7^{-1}-6.7^{-2}}{9}}[/tex], дясната страна сигурно е 2
- martin123456
- Математик
- Мнения: 2395
- Регистриран на: 10 Яну 2010, 18:12
- Местоположение: София
- Рейтинг: 92
Re: ПОКАЗАТЕЛНИ УРАВНЕНИЯ ;( ПОМОЩ СПЕШНО Е !
4
[tex]5^x+5^{x+2}=2^{x+1}+2^{x+2}[/tex]
[tex](\frac{5}{2})^x+(\frac{5}{2})^x25=2+4[/tex]
[tex](\frac{5}{2})^x=\frac{3}{13}[/tex]
[tex]x=\log_{2.5}{\frac{3}{13}}[/tex]
[tex]5^x+5^{x+2}=2^{x+1}+2^{x+2}[/tex]
[tex](\frac{5}{2})^x+(\frac{5}{2})^x25=2+4[/tex]
[tex](\frac{5}{2})^x=\frac{3}{13}[/tex]
[tex]x=\log_{2.5}{\frac{3}{13}}[/tex]
- martin123456
- Математик
- Мнения: 2395
- Регистриран на: 10 Яну 2010, 18:12
- Местоположение: София
- Рейтинг: 92
Re: ПОКАЗАТЕЛНИ УРАВНЕНИЯ ;( ПОМОЩ СПЕШНО Е !
5
[tex]6.4^x-13.6^x+6.9^x=0[/tex][tex]/(6^x)[/tex]
[tex]6(\frac{2}{3})^x-13+6.(\frac{3}{2})^x=0[/tex]
[tex]y=(\frac{2}{3})^x[/tex]
[tex]6y-13+\frac{6}{y}=0[/tex]
[tex]6y^2-13y+6=0[/tex]. [tex]D=169-144=25[/tex]
намери корените
[tex]6.4^x-13.6^x+6.9^x=0[/tex][tex]/(6^x)[/tex]
[tex]6(\frac{2}{3})^x-13+6.(\frac{3}{2})^x=0[/tex]
[tex]y=(\frac{2}{3})^x[/tex]
[tex]6y-13+\frac{6}{y}=0[/tex]
[tex]6y^2-13y+6=0[/tex]. [tex]D=169-144=25[/tex]
намери корените
- martin123456
- Математик
- Мнения: 2395
- Регистриран на: 10 Яну 2010, 18:12
- Местоположение: София
- Рейтинг: 92
6 мнения
• Страница 1 от 1
Кой е на линия
Регистрирани потребители: Google Adsense [Bot], Google [Bot]

 Меню
Меню