Пак неравенство

[Гост]

[tex]x^{3 }+1 \le0[/tex]
Условието е: да се намерят решенията.

Хубу де, постъпих тъй:

[tex](x+1)( x^{2 }-x+1) \le0[/tex]

И от това коренно уравнение, дето няма корени (D<0), какво да го правя? Да го махам ли автоматично? Иначе в сборника пише, че решението е [tex](- \infty; -1)[/tex], ама също и тази скоба ме обърка... Не трябва ли да е квадратна? Или съм прекалено тъпа? надявам се някой отзивчив и по-опитен от мен да ми обясни, мс

[Jack]

[tex]x^{3 }+1 \le0[/tex]
Условието е: да се намерят решенията.

Хубу де, постъпих тъй:

[tex](x+1)( x^{2 }-x+1) \le0[/tex]

И от това коренно уравнение, дето няма корени (D<0), какво да го правя? Да го махам ли автоматично? Иначе в сборника пише, че решението е [tex](- \infty; -1)[/tex], ама също и тази скоба ме обърка... Не трябва ли да е квадратна? Или съм прекалено тъпа? надявам се някой отзивчив и по-опитен от мен да ми обясни, мс

И $-1$ е решение на неравенството, така че трябва да е квадратна скоба. Тоест $(- \infty; -1]$.

[S.B.]

[tex]x^{3 }+1 \le0[/tex]
Условието е: да се намерят решенията.

Хубу де, постъпих тъй:

[tex](x+1)( x^{2 }-x+1) \le0[/tex]

И от това коренно уравнение, дето няма корени (D<0), какво да го правя? Да го махам ли автоматично? Иначе в сборника пише, че решението е [tex](- \infty; -1)[/tex], ама също и тази скоба ме обърка... Не трябва ли да е квадратна? Или съм прекалено тъпа? надявам се някой отзивчив и по-опитен от мен да ми обясни, мс

[tex]x^{3 } + 1 \le 0 \Leftrightarrow (x + 1)( x^{2 } - x + 1) \le 0[/tex]
[tex]x^{2 } - x + 1 > 0[/tex] винаги,защото:
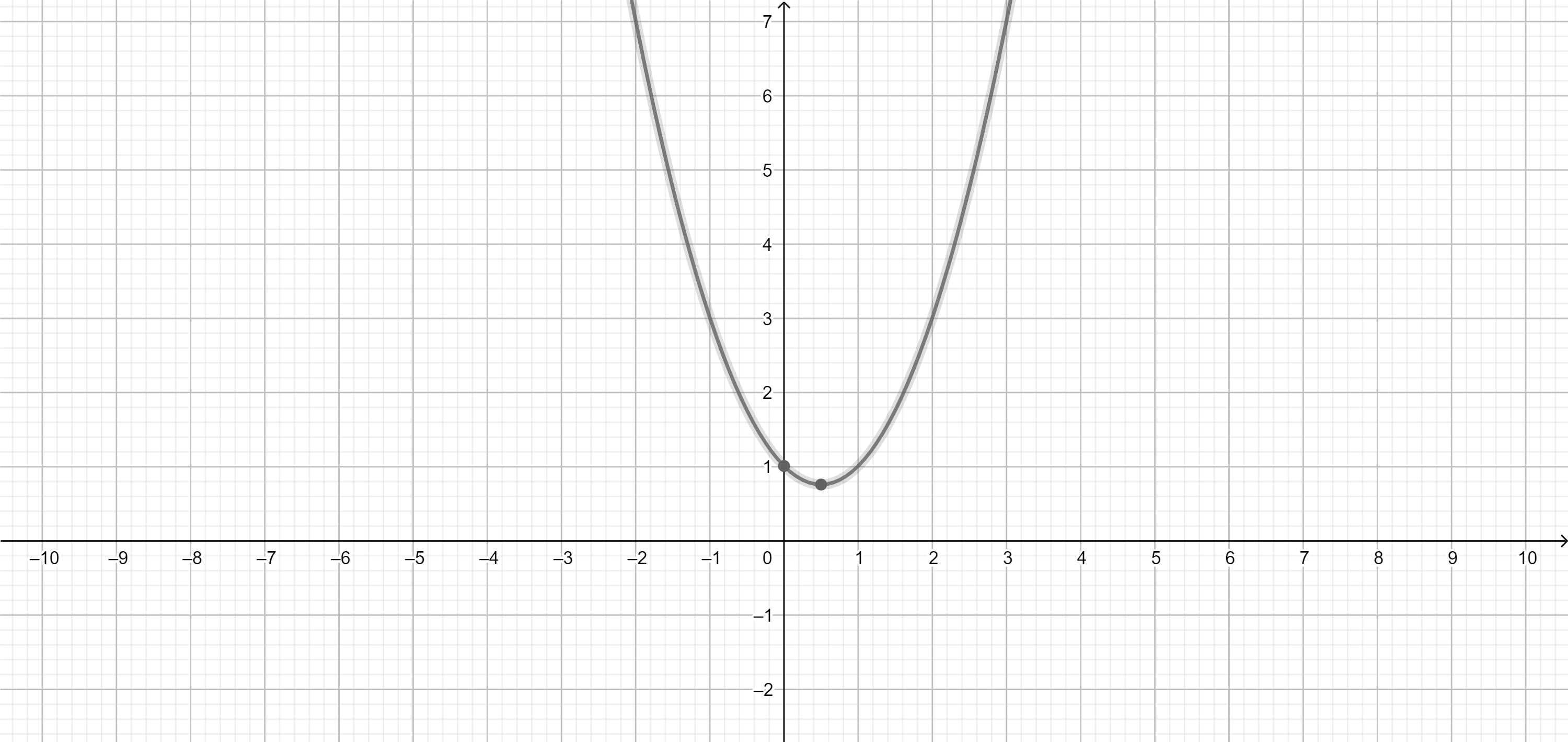
Коефициентът пред [tex]x^{2 }[/tex] е положителен и едновременно с това $D <0$ ,което означава,че графиката на параболата е обърната "нагоре" ,винаги остава над абцисната ос и никога няма да я пресече,защото няма реални корени - т. е. винаги е положителна:

Без заглавие - 2022-03-03T150931.141.png (478.4 KiB) Прегледано 1305 пъти

От[tex]\begin{array}{|l} (x + 1)( x^{2 } - x + 1) \le 0\\ x^{2 } - x + 1 > 0 \end{array} \Rightarrow x + 1 \le 0 \Rightarrow x \le -1[/tex]
Отговорът е: [tex]x \in ( - \infty; -1][/tex]