Приложение на тригонометрията

[Евва]

През върха В и средата на височината CD на [tex]\triangle[/tex]АВС е построена права .
В какво отношение тази права дели лицето на триъгълника ,ако [tex]\angle[/tex]А=[tex]\alpha[/tex] и [tex]\angle[/tex]В=[tex]\beta[/tex] ?

Скрит текст: покажи

Отг. [tex]\frac{sin( \alpha+ \beta) }{sin \alpha.cos \beta }[/tex]

[S.B.]

През върха В и средата на височината CD на [tex]\triangle[/tex]АВС е построена права .
В какво отношение тази права дели лицето на триъгълника ,ако [tex]\angle[/tex]А=[tex]\alpha[/tex] и [tex]\angle[/tex]В=[tex]\beta[/tex] ?

Скрит текст: покажи

Отг. [tex]\frac{sin( \alpha+ \beta) }{sin \alpha.cos \beta }[/tex]

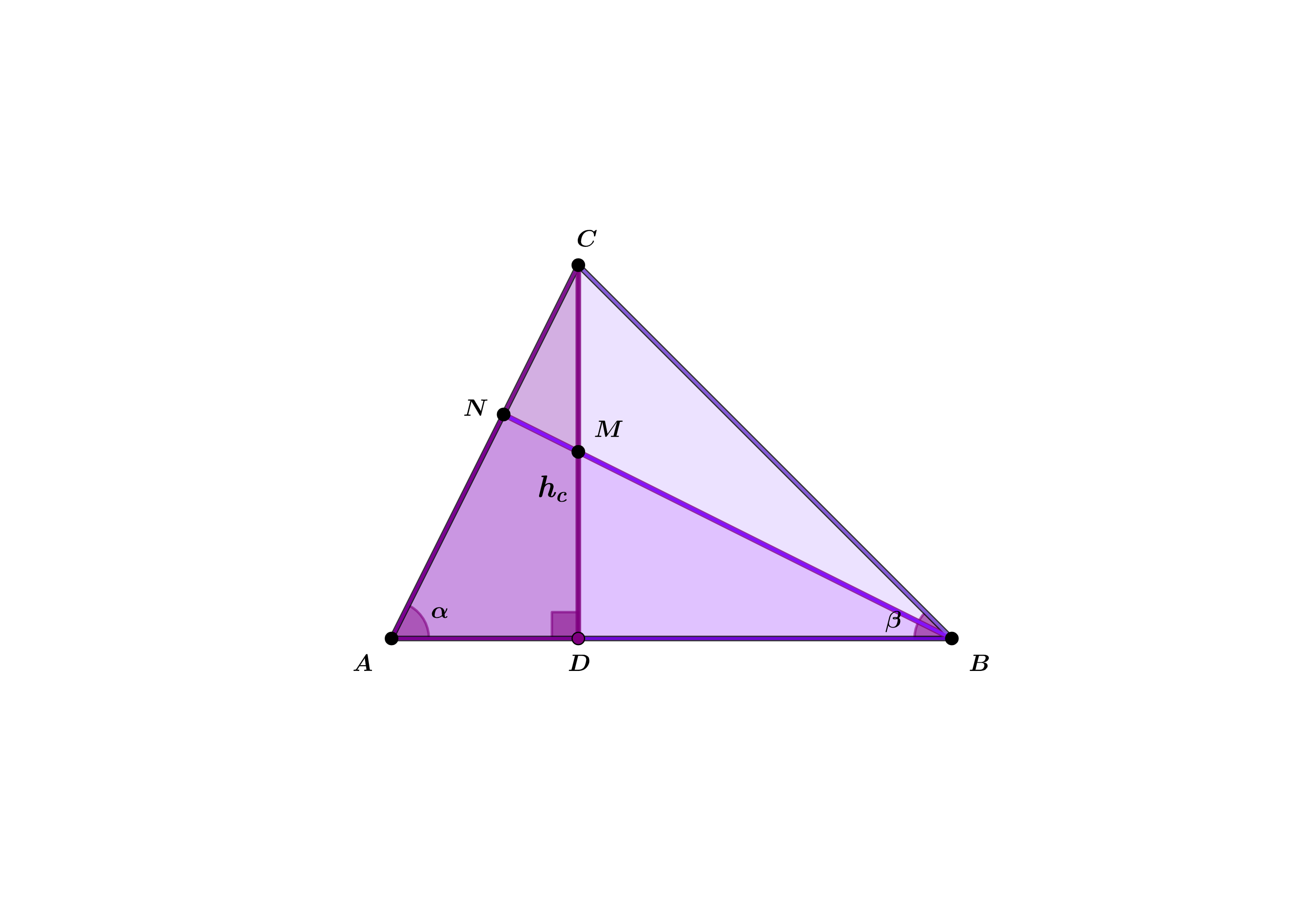
Без заглавие - 2021-09-07T195524.406.png (158.65 KiB) Прегледано 673 пъти

[tex]\triangle ABN[/tex] и [tex]\triangle BCN[/tex] на които правата $BN$ разделя [tex]\triangle ABC[/tex] са с равни височини [tex]\Rightarrow \frac{ S_{ABN } }{ S_{CBN } } = \frac{AN}{CN}[/tex]

За [tex]\triangle ACD[/tex] и правата $BN$ прилагам теоремата на Менелай и Чева:
$$\frac{AB}{BD}. \frac{DM}{MC} . \frac{CN}{NA} = 1$$
По условие [tex]DM = MC = \Rightarrow \frac{AB}{BD}. \frac{DM}{MC}. \frac{CN}{NA} = 1 \Leftrightarrow \frac{AB}{BD}. \frac{CN}{NA} = 1 \Rightarrow \frac{AB}{BD} = \frac{NA}{NC}[/tex]

[tex]\triangle ABC[/tex] и [tex]\triangle DBC[/tex] имат еднакви височини [tex]\Rightarrow \frac{ S_{ABC } }{ S_{DBC } } = \frac{AB}{BD}[/tex]

От [tex]\triangle ADC \rightarrow \frac{AD}{DC} = \cotg \alpha \Rightarrow AD = DC\cotg \alpha[/tex]

Oт [tex]\triangle DBC \rightarrow \frac{DB}{CD} = \cotg \beta \Rightarrow DB = CD\cotg \beta[/tex]

[tex]S_{ABC } = \frac{AB.CD}{2} = \frac{(AD + DB)}{2}.CD = \frac{DC\cotg \alpha+ DC\cotg \beta }{2}.DC = \frac{a\cotg \alpha+ \cotg \beta }{2} CD^{2 } \Rightarrow[/tex]
$$S_{ABC } = \frac{\sin( \alpha + \beta) }{2.\sin \alpha \sin \beta }. CD^{2 }$$
[tex]S_{BDC } = \frac{BD.CD}{2}= \frac{CD\cotg \beta }{2}.CD = \frac{\cotg \beta }{2}. CD^{2 } \Rightarrow[/tex]
$$S_{BDC } = \frac{\cos \beta }{2\sin \beta }. CD^{2 } $$
[tex]\displaystyle\frac{AB}{BD} = \displaystyle \frac{ S_{ABC } }{ S_{DBC } } = \displaystyle \frac{\displaystyle \frac{\sin( \alpha+ \beta) }{2\sin \alpha\sin \beta }. CD^{2 } }{\displaystyle \frac{\cos \beta }{2\sin \beta }. CD^{2 } } = \displaystyle \frac{\sin( \alpha+ \beta )}{\sin \alpha .\cos \beta }[/tex]

Но [tex]\frac{AB}{DB} = \frac{AN}{NC} = \frac{ S_{ABN } }{ S_{CBN } } \Rightarrow[/tex]
$$\frac{ S_{ABN } }{ S_{CBN } } = \frac{\sin( \alpha + \beta )}{\sin \alpha .\cos \beta } $$

[Гост]

Защо Менелай и Чева? Къде е Чева?

[Евва]

Ще чакам решение без теоремата на Менелай .

[Гост]

Ще чакам решение без теоремата на Менелай .

Правилно!Не само без Менелай,но и задължително без чертеж!

[Гост]

Ще чакам решение без теоремата на Менелай .

Правилно!Не само без Менелай,но и задължително без чертеж!

S.B. защо се напрягаш, Ева ти е колежка

[S.B.]

S.B. защо се напрягаш, Ева ти е колежка

Ако имам да кажа нещо на Евва,аз ще ѝ го кажа на Л.С.!С Евва се знаем от много време ,още от времето когато тя беше "Ева" и много пъти сме си писали лични съобщения и на тема чертежи и на много други теми.Можем да си го позволим ,за разлика от теб,който си НИКОЙ в този форум.Аз съм сигурна,че Евва ще представи и своето решение на задачата,което ще бъде интересно.
Гостите в този форум станахте повече от регистрираните потребители.Все пак аз Ви приветствам с добре дошли във форума!Чувствайте се като у дома си,но не забравяйте,че сте на гости!Искам да вярвам ,че вашето посещение в този форум не се изчерпва единствено с неистово желание за хейт, а с нещо по-смислено и градивно.

[Гост]

Е как така час ми говориш на ти, час на Вие? Хванах тe в мишкуване и си загуби граматиката. Друг път няма да пишеш като Гост, за да не разваляш имиджа на гостите.

[Гост]

И какво ми говориш добре дошъл, чувствай се като у дома си, но не забравяй, че си на гости...Аз да не съм дошъл у вас на гости?

[Евва]

Аз означих AN=x ,CN=y и [tex]\angle[/tex]ABN=[tex]\varphi[/tex] .Разглеждаме [tex]\triangle[/tex]ABN и [tex]\triangle[/tex]NBC
[tex]\frac{x}{sin \varphi }[/tex]=[tex]\frac{BN}{sin \alpha }[/tex] и [tex]\frac{y}{sin( \beta - \varphi )}[/tex]=[tex]\frac{BN}{sin[ 180 ^\circ-( \alpha + \beta ) ]}[/tex] [tex]\Rightarrow[/tex]

[tex]\frac{x.sin \alpha }{sin \varphi }[/tex]=[tex]\frac{y.sin( \alpha+ \beta) }{sin( \beta - \varphi )}[/tex]

[tex]\frac{x}{y}[/tex]=[tex]\frac{sin( \alpha+ \beta) }{sin \alpha }[/tex] .[tex]\frac{sin \varphi }{sin( \beta- \varphi )}[/tex] (@)

sin[tex]\varphi[/tex]=? cos[tex]\varphi[/tex]=?
tg[tex]\beta[/tex]=[tex]\frac{CD}{BD}[/tex] и tg[tex]\varphi[/tex]=[tex]\frac{ \frac{CD}{2} }{BD}[/tex] [tex]\Rightarrow[/tex] tg[tex]\beta[/tex]=2tg[tex]\varphi[/tex] [tex]\Rightarrow[/tex] [tex]\frac{sin \beta }{cos \beta }[/tex]=[tex]\frac{2sin \varphi }{cos \varphi }[/tex] (1)

Знаем ,че [tex]sin^{2 }[/tex][tex]\varphi[/tex]+[tex]cos^{2 }[/tex][tex]\varphi[/tex]=1 (2)
Решаваме системата от двете ур-я и получаваме sin[tex]\varphi[/tex]= [tex]\frac{sin \beta }{ \sqrt{4 cos^{2 } \beta + sin^{2 } \beta } }[/tex] и cos[tex]\varphi[/tex]=[tex]\frac{2cos \beta }{ \sqrt{4 cos^{2 } \beta + sin^{2 } \beta } }[/tex]

Скрит текст: покажи

Връщаме се към (@) .

[tex]\frac{x}{y}[/tex] =[tex]\frac{ \frac{sin( \alpha+ \beta) }{1} . \frac{sin \beta }{ \sqrt{4 cos^{2 } \beta + sin^{2 } \beta } } }{ \frac{sin \alpha }{1}[ \frac{sin \beta }{1}. \frac{2cos \beta }{ \sqrt{4 cos^{2 } \beta + sin^{2 } \beta } } - \frac{cos \beta }{1}. \frac{sin \beta }{ \sqrt{4 cos^{2 } \beta + sin^{2 } \beta } } ] }[/tex] = [tex]\frac{sin( \alpha + \beta) }{sin \alpha cos \beta }[/tex]


[tex]\frac{ S_{ABN } }{ S_{NBC } }[/tex]=[tex]\frac{ \frac{x.B B_{1 } }{2} }{ \frac{y.B B_{1 } }{2} }[/tex]=[tex]\frac{x}{y}[/tex]= [tex]\frac{sin( \alpha + \beta )}{sin \alpha cos \beta }[/tex]