Атмосферно налягане на газова планета

[pipi langstrump]

Дадена ни е идеализирана газова планета, която се състои изцяло от газ, който можем да смятаме за идеален. Приемаме, че температурата на газа е еднаква навсякъде и, че газът навсякъде има един и същ състав. Знаят се температурата и моларната маса на газа, както и масата на планетата. Задачата е: да се намери атмосферното налягане на планетата като функция на разстоянието до центъра й.

[ptj]

Използваме уравнението на Клапейрон-Менделеев за идеален газ:
[tex]p.V=\frac{m}{M}RT[/tex]

[tex]V=\frac{4\pi r^3}{3}[/tex] , където [tex]r[/tex] е радиуса на кълбото (планетата)

[tex]p=\frac{mRT}{MV }=\frac{3mRT}{4\pi Mr^3 }[/tex]

[pipi langstrump]

Имаш сериозна грешка в използването на уравнението на идеалния газ, която е довела и до физически неприемлив резултат - няма как налягането да е едно и също из цялата планета.

[ptj]

Доколкото си спомням в идеален газ при постоянни температура и обем, налягането също е константа, т.е. еднакво е във всяка материална точка (частица на газа).

[pipi langstrump]

Когато газа е в термодинамично равновесие или участва в квазистатичен процес и не е подложен на действие на силови полета (без значение дали външни или вътрешни), тогава налягането е еднакво във всяка точка от обема, който той заема

[pipi langstrump]

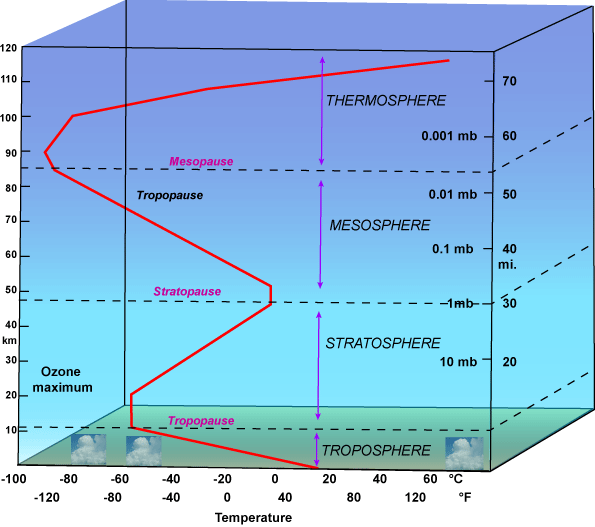
От тая картинка се вижда, че в земната атмосфера температурата не е монотонна функция на височината, но налягането е намаляваща. Има и области с една и съща температура, но в които налягането е различно. Защо?

[ptj]

Имам въпрос:

Под идеализирана газова планета, не се ли разбира планета състояща се само от газ, в която вътрешните и външни сили се пренебрегват?

Защото при примера с земната атмосфера, мисля че решаващо значение има наличието на относително голяма сила на тежестта (гравитация) заради масата на твърдото тяло в центъра (земята).

[pipi langstrump]

Под идеализирана имах предвид, че приемаме, че се състои от идеален газ и има еднаква температура навсякъде. Гравитацията се създава от самия газ.

П.П. Може би протозвездата е по-близко до тая идеализация, отколкото някоя газова планета.

[pipi langstrump]

Записваме закона на Клапейрон в локална форма

[tex]p=\frac{1}{\mu}\rho RT \space{(1)}[/tex]

където [tex]p, \rho[/tex] са скаларни полета - функции на мястото.Температурата също е скаларно поле но в случая сме приели, че е константа.
От друга страна от условието за хидростатично равновесие имаме

[tex]\nabla p = \rho g[/tex] или
[tex]p'(r) = \rho g \space{(2)}[/tex]
понеже [tex]p(\vec{r}) = p(r)[/tex]

Трета връзка между [tex]g[/tex] и [tex]\rho[/tex] имаме от закона за гравитацията

[tex]g(r) = \frac{GM(r)}{r^2} = \frac{G}{r^2}{\int\limits_{0}^{r}\rho(z)4\pi z^2dz} \space{(3)}[/tex]

Три уравнения, три неизвестни функции [tex]p[/tex], [tex]\rho[/tex] и [tex]g[/tex].

[Sup3rlum]

Интересна задача

$P=\frac{k}{\mu}\rho T$ което при хомогенен състав и постоянна температура означава, че можем да използваме $P=\frac{kT}{\mu}\rho \Rightarrow P'=\frac{kT}{\mu}\rho '$

$P'=\rho g\Rightarrow \frac{kT}{\mu}\rho'=\rho g$

Разделимо диференциално уравнение:

$\frac{kT}{\mu}\frac{\rho'}{\rho}=g$
$\rho=\rho_0e^{\frac{\mu}{kT}\int_0^rg(x)dx}$
$P(r)=P_0e^{\frac{\mu}{kT}\int_0^rg(x)dx}$

Има тривиална форма за константен гравитационен профил $g(r)=const$
За Нютонов гравитационен профил $g(r)=\frac{4\pi G}{r^2}\int_0^r x^2\rho(x)dx$ мисля, че затворена форма няма, защото се получава нелинейно диф уравнение от 4-та степен спрямо $\rho$, но не се и съмнявам, че има и уловка

[pipi langstrump]

Пропуснал съм един минус в (2). Трябва да е [tex]p' = - \rho g[/tex]

Не знам каква уловка може да се измисли.
Уравнението в компактна форма изглежда така:

[tex]((\ln \rho(r))'r^2)' = -Ar^2 \rho(r)[/tex]

Ако положим [tex]\ln \rho = h[/tex], добива по-проста форма

[tex]h'' + \frac{2h'}{r} + Ae^h = 0[/tex]

но и така ми изглежда нерешимо. Най-много можем за достатъчно големи r да пренебрегнем средния член и да намерим асимптотично решение. Ако не съм сбъркал нещо в сметките, за тази случай се получава

[tex]\rho_{asympth}(r) = \frac{C}{2A} \operatorname{sech}^2 \left(\frac{\sqrt{C}r}{2}\right)[/tex], където константата C по принцип се намира от условието [tex]\int\limits_{0}^{\infty}4\pi z^2\rho (z)dz = M[/tex], ако [tex]\rho (r)[/tex] беше истинската функция, но за асимптотичната трябва да знаем масата от някаква височина [tex]r_0[/tex]нагоре, за която сме приели, че функцията вече е валидна, т.е. [tex]M_{r_0} = \int\limits_{r_0}^{\infty}4\pi z^2\rho (z)dz[/tex]

С директни сметки можем да проверим и, че [tex]\frac{2h'}{r}[/tex] действително клони към нула и то със скорост 1/r.

[peyo]

Под идеализирана имах предвид, че приемаме, че се състои от идеален газ и има еднаква температура навсякъде. Гравитацията се създава от самия газ.

П.П. Може би протозвездата е по-близко до тая идеализация, отколкото някоя газова планета.

Чудех се доколко е възможно(/реално) да искаме температурата на газа да е еднаква навсякъде?

Температурата на идеалния газ нали е пропорционална на кинетичната енергия на газа? Тогава под влиянието на гравитацията концентрацията на газа около центъра ще е по-голяма и броя на молекули и от там енергията в единица обем трябва да е по-голяма отколкото по-далече от центъра, което влече разлика в температурата.

[pipi langstrump]

Температурата на газа не зависи от енергията му в единица обем. Пример пак от земната атмосфера - в нея има област, наречена термосфера, където температурата достига до 2500°С, но газът е толкова разреден, че един термометър би измерил 0°С. Съответно и енергийната му плътност е ниска, въпреки високата температура.
Да погледнем пак уравнението на идеалния газ за температурата

[tex]T = \frac{p \mu}{\rho R}[/tex]

Виждаме, че ако налягането и плътността се изменят по един същ начин така, че отношението им да е постоянно, тогава и температурата ще е постоянна. Голямата плътност в центъра ще се компенсира от голямото налягане и температурата може да остане същата както и далече в горните пластове. Доколко обаче наистина е възможно такова константно разпределение на Т? Не само че е възможно , но е и задължително за една планета/протозвезда, в която се е възцарило термодинамично равновесие. Според втория закон на термодинамиката всички части на системата се стремят към температурно изравняване или което е еквивалентно - системата се стреми към състояние с максимална ентропия.