 от ammornil » 09 Яну 2013, 15:17
от ammornil » 09 Яну 2013, 15:17
[tex]\begin{array}{|l} y=x^2+5x \\ x= y^2+5y \end{array}[/tex]
Ако заместим х от второто уравнение в първото ще получим:
[tex]y=x.(x+5)=(y^2+5y).(y^2+5y+5) \\
y=y^4+5y^3+5y^2+5y^3+25y^2+25y \\
y^4+10y^3+30y^2+24y=0 \Leftrightarrow y.(y^3+10y^2+30y+24)=0 \\
y.(y^3+10y^2+30y+24)=0 \Leftrightarrow y.(y^3+4y^2+6y^2+30y+24)=0 \\
y.[y^2.(y+4)+6.(y^2+5y+4)]=0 \Leftrightarrow y.[y^2.(y+4)+6.(y+4).(y+1)]=0 \\
y.(y+4).(y^2+6y+6)=0 \Leftrightarrow y.(y+4).(y+\frac{3-\sqrt{3}}{2}).(y+\frac{3+\sqrt{3}}{2})=0[/tex]
[tex]\begin{array}{|l}y_1=0 \\ x_1=0 \end{array} \hspace{4 mm} \cup \hspace{4 mm} \begin{array}{|l}y_2=-4 \\ x_2=-4 \end{array} \hspace{4 mm} \cup \hspace{4 mm} \begin{array}{|l}y_3=\frac{-3-\sqrt{3}}{2} \\ x_3=\frac{-9-2\sqrt{3}}{2} \end{array} \hspace{4 mm} \cup \hspace{4 mm} \begin{array}{|l}y_4=\frac{-3+\sqrt{3}}{2} \\ x_4=\frac{-9+2\sqrt{3}}{2} \end{array}[/tex]
---
Геометрично погледнато това са две параболи, първата с ос на симетрия успоредна на оста Oy, а втората с ос на симетрия успоредна на оста Ox. Решения на системата са пресечните точки на двете параболи. От графиката се вижда, че имаме четири решения.
- Прикачени файлове
-
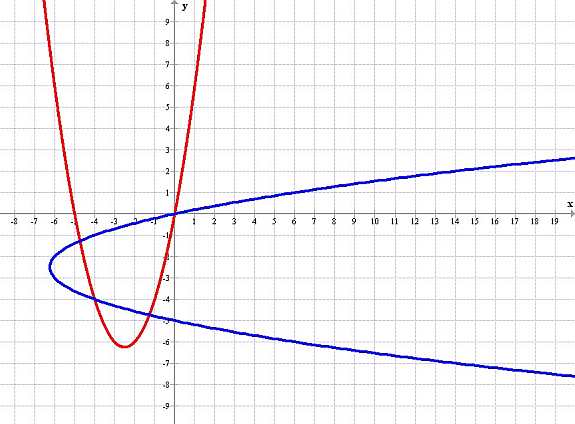
- paraboli.jpg (28.67 KiB) Прегледано 801 пъти
[tex]\color{lightseagreen}\text{''Който никога не е правил грешка, никога не е опитвал нещо ново.''} \\
\hspace{21em}\text{(Алберт Айнщайн)}[/tex]