Забавна математика - хитроумни задачи

1. един стар сборник от задачи "Присъдата на Парис" е описана задача по следния начин: Богините Хера, Афродита и Атина запитали умния Парис коя от тях е най-красива. Предварително те казали следното:
Афродита: Аз съм най-красивата.          (1)
Атина: Афродита не е най-красивата.        (2)
Хера: Аз съм най-красивата.           (3)
Афродита: Хера не е най-красивата.         (4)
Атина: Аз съм най-красивата.          (5)
Парис, който си почивал край пътя, не счел за нужно да махне кърпата, която покривала очите му, пазейки ги от сленчевите лъчи. Той обаче бил длъжен да определи коя точно от трите богини е най-красива. Той допуснал, че изказванията на най-красивата са верни, а всички твърдения на другите две богини са неверни. В състояние ли е бил Парис при това допускане да произнесе изискваната от него присъда? Ако е бил, какво гласяла тя?

2. "Абракадабра" е вълшебна дума, която в древността са гравирали в амулети, за да предпазва носещите ги от болест и зла участ. Дали сега ще използваме думата "Математика" - разчленена по друг начин - въпросът е един и същ:

По колко начина може да се прочете всяка от двете думи?

3. "За къде си се разбързал?"
"За влака в 6h. Колко минути остават до тръгването му?
"Преди 50 минути от 3h насам бяха изминали четири пъти повече минути,отколкото сега остават до 6h."
Колко е бил часът?

4. На обяд около масата са седнали един дядо, една баба, двама бащи, две майки, четири деца, три внука, един брат, две сестри, двама сина, две дъщери, един свекър, една свекърва и една снаха. Колко най-малко чинии са необходими?

5. Пет момичета са седнали в метрото едно до друго. Анет е отдалечена от Бабет точно толкова, колкото и от Колет. Дорет седи на такова разстояние от Анет, на каквото и от Колет. Между кои от своите приятелки пък е седнала хубавата Жанет?

6. За да открием намислено естествено число, го умножаваме със следващото го по големина в естествения ред на числата и от произведението вадим намисленото число. Как от този резултат се получава търсеното число?

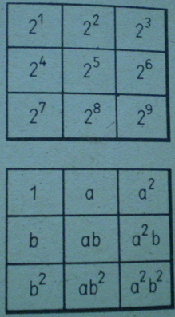
7. а) В горния магически квадрат деветте степени трябва да се подредя така, че произведенията по всеки ред, стълб и диагонал да бъдат едни и същи. Кой ще стори това най-бързо?
б) В долни я магически квадрат деветте члена трябва да се подредят така, че произведенията по всеки ред, стълб и диагонал да бъдат равни на а³b³. Положете след това а = 2 и b = 3.

9. Ханс разказва: "четирицифреният номерна колата на учителя ми по математика е много лесен за запомняне. Той е симетричен, а сборът от цифрите му е равен на числото, съставено от първите му две цифри." Кой е номерът на колата?

10. Моника казва на Мария-Луиза: "Кажи ми едно трицифрено число, цифрите на копет са две по две различни и между тях няма нула, Напиши го и под него запиши всички трицифрени числа, които могат да се получат при разместване на цифрите на назованото число!" Преди още Мария-Луиза да успее да намери сумата, Моника вече й казала резултата. Как е могла да получи отговора толкова бързо?

11. Aнглийския автор на занимателни книги по математика Барнард нарича тази, известна в ГДР като "игра на вятъра" система Еквилиабър (това понятие е образувано от думите Еквилибристика и Канделабър).
Kои два предмета, поставени на мястото на въпросителнта, ще поддържат системата (съставена от рибки, топки, камбанки и хоризонтални летвички, съответни техни комбинации) в равновесие? при това за разлика от хоризонталните летвички теглото на конците не се взима под внимание.

12. При една игра игра със зар е в сила следното правило: Ако се падне четно число, се получават толкова положителни точки, колкото показва зарът. Обърне ли се обаче зарът на нечетно число, съответните стойности се записват като отрицателни точки. Някой хвърлил зара пет пъти един след друг; две от числата били равни, а останалите се различавали едно от друго. Накрая положителните и отрицателните точки се унищожили. Кои числа са се паднали?

13. Потърсете дали има естесвени числа, притежаващи следните свойства:
Ако едно такова число разделим
с 3, ще получим остатък 1,
с 4, ще получим остатък 2,
с 5, ще получим остатък 3,
с 6, ще получим остатък 4.
Ако такива числа съществуват, да се посочи най-малкото естесвено число, притежаващо тези свойства.

14. Числата 12 и 60 имат интересно свойство. Поризведението им е десет пъти по голямо от сумат им.
12.60 = 720 и 12 + 60 = 72.
Съществуват ли и други подобни двойки естесвени числа?