Футболистите струват милиони, математиците се подаряват!

Васил Шумаров

Преди няколко месеца изразих мнение, че не смятам теста за най-удачната форма за приемен изпит по математика (същото бих казал и за изпит по литература). Нямам представа колко от колегите-учители по математика споделят това мнение, но Министерството явно е твърдо решено да реализира всичките си замисли, независимо от всякакви частни становища.

Първите тестови изпити за елитни гимназии минаха при безупречна организация, включително раздаване на специални листове и писалки. Тестът по математика ще влезе в историята с 1200 двойки и само две пълни шестици. И още – с незабавната гневна реакция на ученици, на родители, учители и журналисти. Особено съм впечатлен от едно интервю в регионален вестник на двама пернишки колеги – Георги Михайлов и Катя Сабадошева, които определят съдържанието на теста като „подигравка с труда на преподавателите и учениците, своеобразна наказателна мярка на просветното министерство” след учителските протести срещу ниските заплати. Аз също смятам, че тестът като цяло е прекалено труден и направо невъзможен за лимита от 3 часа. А когато никой не може да се справи, изчезва разликата между онези учители и ученици, които са работили и онези, които не са работили.

Понеже за тройка са достатъчни 16 от 100 възможни точки, а първите 14 въпроси и задачки бяха повече от лесни, броят на двойките трябва да се счита за конфузно голям, но аз не мисля, че за това са виновни учителите. Защото не може да се иска от тях да научат на алгебра и геометрия Сульо и Пульо, които така и не са могли да проумеят, че две на степен трета не е две по три!

Оставяйки за друг път темата доколко е полезно да измъчваме споменатите Сульо и Пульо с въпроса за дефиниционната област и графиките на функциите тангенс и котангенс, сега бих искал да обърна внимание не на двойките, а на отличните оценки, две от които кръгли шестици (едната на софийски, другата на пловдивски ученик).

Ще приема минималният брой на отлични работи като доказателство, че не е имало изтичане на информация за съдържанието на тестовете, така че отличниците са просто едни надарени и отлично обучени (!) българчета, които за три часа време са „прегазили” 50 задачи, половината от които трудни и много трудни! Голямо или малко е това постижение на техните учители? За да не говорим с общи приказки, нека разгледаме няколко конкретни примери от теста. Да започнем с една от задачите, на които обръщат внимание колегите Михайлов и Сабадошева заради това, че се решават чрез „алогични допълнителни построения”, т.е. чрез допълване на чертежа с помощни отсечки и фигури, които не следват от никаква логика.

(Във вестника е записано „аналогични построения”, но това навярно е обичайната репортерска „корекция”. Репортерките, както знаем, са особена порода: ако им кажеш, че Ръдърфорд е разложил атома, ще напишат, че е „разположил атома”, ако кажеш „макроскопични параметри”, ще напишат „микроскопични параметри”, ако кажеш, че директорът е поискал маломерни паралелки, ще напишат „маломерни парцели”, ако кажеш, че някой е бил отлъчен от колектива, ще напишат, че е бил „отличен от колектива”, ако кажеш, че шлейфовете на римските патриции понякога са били дълги 12 метра, ще напишат, че „шлемовете им са били дълги 12 метра” и прочие професионални чудеса, които извадих от моя личен архив). И така, започваме със задача 49 от теста.

49 (3 т.) Даден е успоредник ABCD, в който AB = 2 AD. Нека М е средата на страната АВ и DP BC (P BC ). Да се намери BAD, ако MPB = 50°.
Дадено: AD = AM = MB = BC = a, DP BC, MPB = 50°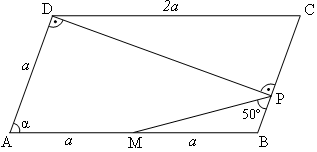




Търсим: A = α = ?
Решение:
Срещуположните ъгли на успоредника са равни: C = A = α. Търсеният ъгъл α участва в правоъгълен триъгълник CDP. Ако означим другия остър ъгъл на триъгълника например с ε, ще имаме α + ε = 90° (тъй като третият ъгъл на триъгълника е 90°). Значи задачата се свежда до намиране на ъгъл ε. Ако свържем точка А с Р, ще имаме още един правоъгълен триъгълник APD, но той очевидно не е еднакъв със CDP и няма да ни помогне. Триъгълникът MBP има един ъгъл от 50° и една страна a, но не е правоъгълен и няма нищо общо с CDP. Тогава накъде?

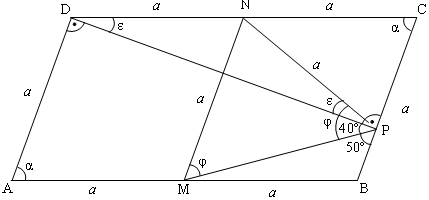
И тук, ей така, както си гледа към тавана, 14-годишният кандидат-гимназист трябва изведнъж да си каже: Абе що не взема да намеря средата на отсечката DC, да я означа например с буква N и да я свържа с точка М. Тогава ще имаме два еднакви ромба; AMND и MBCN със страна а и от това може да излезе нещо полезно? Речено-сторено! И започва да прекарва диагоналите на тези еднакви ромбове и да се върти в кръг, за да разбере накрая, че и от това нищо не излиза. И тъкмо да захвърли листа, в главата на нашия седмокласник изневиделица възниква втора идея: А какво ли ще е, ако свържа точка Р с точка N? Бинго!!! Това ще е медиана към хипотенузата CD на правоъгълен триъгълник CDP, а според известната на цялата международна общност теорема такава медиана е равна на половината от хипотенузата, т.е. на всяка от двете равни части, на които я разделя! И ще имаме верижното равенство PN = DN = NC = a, т.е. CDP е равнобедрен и ъглите при основата му са равни помежду си: DPN = PDN = ε.

След още едно закъсване и взиране в тавана, нашият седмокласник ще трябва още веднъж да се плесне по главата, когато се сети, че и триъгълник MPN е равнобедрен с бедра MN = PN = a, следователно и неговите ъгли при основата са равни: NPM = PMN = φ и тогава ще имаме ε = φ - 40°.

Е да, ама като не знаем колко е ?, всичко е напразно! И ето – за четвърти път Добрата Фея го целува по челото и той подскача от радост: успоредните прави MN и ВС са пресечени с трета права MP и в тази конструкция φ и MPB = 50° се явяват кръстни, значи са са равни: φ = 50°. Тогава
ε = 50° - 40° = 10° и накрая: α = 90° - 10° = 80°.

За да стане още по-ясно трудна или лесна е тази задача, нека погледнем в експресното решение, предложено от самите съставители на теста – специалистите на МОН (решението е дословно препечатано от интернет):

Решение: Нека N е средата на DC, тогава MN = BN = BC = NC и BCPMN. Следователно MPB = PMN = MPN = 50° и MNB = NBC = BCN = 180° - 100° = 80°.

Това е цялото решение! По-точно имитацията на решение. Защото, дори и да приемем за машинописна грешката в първия ред, където вместо BN е написано ВМ, остава загадката в третия ред: че NBC = BCN. Това щеше да е вярно, ако страните срещу тези ъгли също са равни: ако NC = BN = a, т.е. ако триъгълникът NBC е равностранен със страна а. Ъглите на такъв триъгълник обаче са по 60°, значи ъгъл α щеше да е 60, а не 80°.

Колегите от Перник отбелязвят в интервюто си, че често при грешен път се получава верен отговор” Ако имахме класически изпит-тема, при който се проверява целия ход на решението, записано на белова, за такова решение, изкарано дополовина, щяхме да дадем половината от предвидените точки. Сега обаче оценяваме тест, при който се гледа само отговора и нищо друго (а той е верен: α = 80°), така че за тази задача трябва да дадем всичките предвидени три точки. Така инспекторите от МОН получават 3 точки за едно силно дефектно решение, само защото предварително са знаели отговора! Върху същата особеност на тестовия изпит аз обърнах внимание в изказаното преди няколко месеца лично мнение по въпроса.

За да не оставя впечатление, че съм се възползвал от единствената неволна грешка в „експресните” решения на инспектората на МОН, ето още две такава:

23 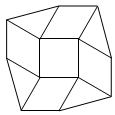(2т.) Фигурата на чертежа е съставена от един квадрат в центъра, четири ромба с равни остри ъгли и четири триъгълника. Да се намери лицето в квадратни сантиметри на всеки от ромбовете, ако лицето на квадрата е 36 кв.см., а лицето на цялата фигура е 204 кв.см.

Решение: Страната на квадрата е равна на 6 cm (т.е. и стените на ромбовете и катетите на триъгълниците са равни на 6 cm) Сумата от лицата на триъгълниците е равна на 4.(6.6)/2 = 72 cm². Тогава сборът от лицата на ромбовете е 204 – (72 + 36) = 96 cm². Следователно лицето на всеки ромб е равно на 24 cm².

Добре, но на какво основание решихме, че бедрата на триъгълниците са катети, т.е. че имаме правоъгълни триъгълници? Колкото и да е „експресно” едно решение, в него не може да отсъства такава важна аргументация – защо въпросните триъгълници са именно правоъгълни. „Прескачането” на аргументация е много разпространен дефект в ученическите писмени работи (и не само по математика), познат на всеки учител. При тестово оценяване и за това дефектно решение инспекторите ще трябва да получат предвидените 2 точки, тъй като отговорът им е верен!

42(2т) Във финала на състезание по бягане на 800 метра участвали шестима ученици от седми клас. Андрей завършил състезанието след Борис и след още двама състезатели. Виктор финиширал след Димитър, но преди Георги. Димитър изпреварил Борис, но не могъл да изпревари Евгени. Кое от момчетата е заело трето място?

Това условие не отговаря на изискванията за математическа строгост. Освен това има недопустим дефект – преопределеност, т.е. съдържа повече дадености, отколкото е необходимо, за да се отговори на зададения въпрос. И ето защо:

По законите на математическата (а не на житейската!) логика първото изречение дава информация, че в състезание по бягане са участвали шестима седмокласници, но това не означава, че освен тях не е имало и други състезатели. (Това може да подведе учениците, особено като се има предвид, че състезанията обикновено се провеждат не по класове, а по възрастови групи). При наличие на други състезатели обаче задачата е нерешима!

Нека приемем, че изтерзаният кандидат-гимназист е проумял това и се е заел да решава задачата при условие, че участници в бягането са само шестимата, чиито имена са изрично споменати. Тогава второто изречение трябва да означава две неща: че Андрей е финиширал четвърти и че Борис е в първата тройка. Четвъртото изречение ни указва, че Димитър и Евгени са преди Борис. И тъй като Борис е в първата тройка, то той е финиширал трети. Това е отговора на зададения въпрос.

Но защо ни е тогава третото изречение: че Виктор финиширал след Димитър, но преди Георги? Нашият кандидат-гимназист, за разлика от бегачите на 800 метра, ще започне да се терзае, да се съмнява в решението си и прочие съклетисвания, които ще му изядат сума ти време. Защото той едва ли може да допусне, че условието на задачата е недогледано и третото изречение е просто излишно!

А аз си мисля, че тази задача е преписана едно към едно от някой сборник, но в оригиналния u вариант се иска да се намери цялостното подреждане на шестимата състезатели, при което третото изречение е необходимо. Това подозрение се усилва от дефектното решение, дадено в сайта на МОН:

Решение: За удобство можем да означим момчетата с А, Б, В, Г, Д и Е (и нека записът АБ означава, че Б е преди А). Тогава от условието получаваме АБ, ГВД и БДЕ. Можем да обединим първото и третото и получаваме АБДЕ. От условието следва, че А е четвърти, тогава останалите двама, Г и В са след А, т.е. подредбата е следната: ГВАБДЕ, т.е. трети е бил Борис.

Като оставим настрана, че подобни (силно формализирани) решения може да са полезни за обучение на бъдещи математици, но не и за развиване на логическото мислене изобщо, самото решение потвърждава казаното по-горе. Защото и тук условието ГВД не е използвано, за да се направи извода АБДЕ, от който направо следва, че третият е Борис.

Дължа да подчертая, че изключвайки тези три пропуска, аз съм силно впечатлен от условията на задачите от втората половина на теста. Намирам ги за много интересни, кратки и остроумни и мисля, че по-добри не може да се измислят и трябва да отдадем заслуженото на съставителите им. Принципното ми възражение е само по дозирането на трудността на решенията и несъответствието с ограниченото време от 180 минути. Инспекторите обаче с пълно основание могат да кажат, че просто са изпълнили указанието на г-н Министъра, което той заяви на всеослушание – да съставят тест, в който лесните задачи да са още по-лесни от досегашните, а трудните – още по-трудни.

След толкова дългото отклонение, нека се върна на основната си мисъл – за труда на преподавателите, чиито ученици са се справили отлично с този много труден тест. Обективната преценка изисква преди всичко да се опише обстановката, в която работи днешното училище. А то работи в една изключително неблагоприятна, бих казал киселинна среда, която унищожава безмилостно труда на учителите! Имам предвид това, че днешният ученик е буквално залят от лавина ярки примери на преуспели мутри, манекени и всевъзможни „топ-модели” от „Плейбой” и „Максим”, спортисти и треньори с договори за половин милион годишна заплата без премиите (говоря за работещите в България), шоумени, които само с едни пезевенкски вицове и долнопробни скечове „заработват” 50 000 лв месечно, и прочие знаменитости, набарали на баницата мекото. Имам предвид разбира се и мръсния потоп визуална и словесна порнография от сайтовете на интернет, а също от телевизията, под формата на т.н. „еротика”, който мачка, промива и деформира съзнанието на децата още от предучилищна възраст. След като се е нагледал на видеофилми с голи разчекнати свои връстнички, които се друсат и викат, подражавайки на какичките-професионалистки, юношата, препълнен с пресни впечатления и „емоции”, пристига в училището, където учителят ще му говори за неземната красота на онова ефирно създание, цялото облечено в бяло, отрупано със сини и червени панделки, със златна коса, пусната свободно по плещите, наречено Ангелинка. На същият този порно-видео-тинейджър учителят трябва да внуши любов към науката! Как мислите, лесно ли е това?

Ето защо аз смятам, че всеки от онези малко на брой педагози, чиито възпитаници са решили теста за отличен, е по ценен за България от Пенев и Мъри Стоилов, взети заедно! Ние дори не сме ги виждали, не знаем имената им. Защото медиите обсъждат и показват само това, което е интересно на журналистите. А на журналистите им е интересно всичко друго, само не и педагогиката. И съвсем никак точни науки. В паметта на един журналист от математиката е останал само спомен за някаква досадна питагорова теорема. От физиката се помни само „Кой не знае закона на Ома, да си оди дома!”, а също „Закона на Нютон за действието и противодействието”, но в смисъл, че ако ти ударят шамар, трябва да отвърнеш с ритник. Журналистите са убедени, че астрологията е раздел от астрономията и хабер си нямат, че със специалната почит към хороскопите всъщност са върнали средновековието.

Прочее, Канал 1 наскоро показа един жив учител по математика, създал олимпийски шампиони - в двуминутен репортаж за юбилейното тържество на Софийската математическа гимназия, филиал на СУ „Св.Климент Охридски”. Това беше един възрастен човек, който скоро ще се пенсионира и тъй като пенсията му ще е 120 лева, за да преживее, ще трябва да дава частни уроци – по 5 лв на час, така че за 100 хиляди часа, т.е. за 12 500 работни дни ще изкара 500 хиляди лева, колкото е годишният доход на един футболен треньор в България. Та този истински народен будител пожела на своите възпитаници успешен път в живота. А „пътят” се оказа презокеански, защото шампионите да един заявиха, че заминават да учат в чужбина, най-вече в Америка. Там щели да им дадат стипендии и им се осигурявали най-добри условия за развитие.

Странно, нали? Същите тези преподаватели, които са създали от младите хора олимпийски шампиони по математика и физика, се оказват неспособни на им създадат условия за по-нататъшно развитие! Това разбира се не е вярно. И всички тези талантливи младежи отлично разбират, че ако проблемът беше само в по-нататъшното овладяване на науката, нямаше да се налага да напускат София. Но те отиват в Америка не само заради науката, а за да останат там завинаги! Това е печалната истина, която трябва да кажем на глас. Техните деца ще поназнайват малко български, а внуците им няма да знаят нито дума. Тук му е мястото да си кажа еретичното мнение, че не е кой знае каква гордост, че създателят на първия електронен компютър е от българско потекло, след като бащата на този велик изобретател – Иван Атанасов е пристигнал в Америка на 13-годишна възраст (с чичо си, защото родителите му са избити в Априлското въстание), а майка му е американката Iva Lucena Purdy. Трите имена на прочутия ни „сънародник” са Джон Винсент Атанасов и той е израснал с още четирима братя-„българи”: Теодор, Ейвис, Реймънд, Ървинг и три сестри-„българки”: Еделин, Маргарет и Мелва, които я са знаели, я не стотина думи от бащиния си език (майчиният им е бил английски или може би италиански, ако се съди по името на майката)

Та така – сиромашка България и до днес продължава да „подхранва” Америка с най-надарените си деца. Напълно безкористно!

Нека най-после формулирам основната си мисъл която не ми дава мира напоследък. Когато някой чуждестранен отбор по футбол например иска да вземе момче от наш отбор, ние не можем насила да спрем трансфера, но това момче си има точно определена цена, която трябва да се внесе в касата на отбора. След което българчето си заминава поживо-поздраво в желания отбор да изучи „висшия пилотаж” на футболното изкуство.

Юридическата пречка същата процедура да се приложи за олимпийския ни отбор по математика навярно е, че това противоречи на принципите на олимпийското движение. Тогава обаче възниква въпросът защо ни е да участваме в такова движение, след като единственият резултат е, че си показваме кои са най-добрите ни млади математици и физици, та да ни ги вземат американците?

А това си е по-лошо от турско! Защото турците са вземали за еничери най-здравите деца, а американците ни вземат най-умните, макар и не с груба сила а със силата на парите.

А не можем ли по дипломатически път просто да им кажем: Многоуважаеми братя американци, много се извиняваме, но нашите олимпийски състезатели по математика и физика са ни много ценни, затова, когато ни ги взимате чрез изкушения, бъдете така добри да преведете за всеки от тях поне 5 милиона долара. Само не казвайте, че е скъпо, защото ние знаем, че военният ви годишен бюджет е 450 милиарда долара и е грехота да ни изсмуквате безплатно най-добрите мозъци под претекст за свободата на движение на хората. А ако все пак държите на безплатни мозъци, то вземете си колкото искате от останалите младежи, които не са олимпийски състезатели!

Ето така ще се сложи някакъв ред и ще се знае, че и трудът на учителите може да струва милиони. Ако някой радетел на свободата на личността ми възрази, че покупко-продажбите създават пречки в развитието на младежите, бих го посъветвал да отиде при футболните треньори да му обяснят играта. Те много отдавна проумяха, че освен олимпийски, трябва да създадат и професионален футбол, за да може трудът им да се цени. Прочее оттогава футболът стана сто пъти по-популярен!

А демагогията около честването на деня на народните будители - 1 ноември може да си остане. Вярно е, че тя нищо не помага, но пък и не пречи.

Васил Шумаров