Върховете(на малките и големите оси) и ексцентрицитета на елисата $\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$ са:
(с $CV_1, CV_2$ сме означили върховете на малката ос)
Решение:
Отговор: $V_{1}(-4,0),V_{2}(4,0);\ CV_{1}(0,-2),CV_{2}(0,2);e=\frac{\sqrt{3}}{2}$
$\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$
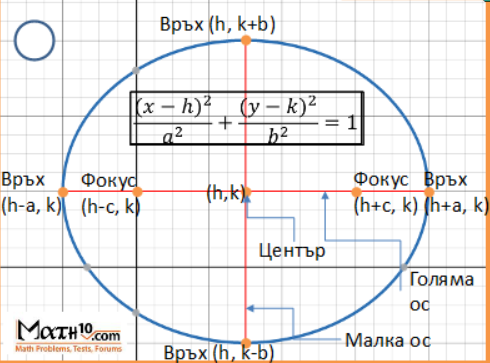
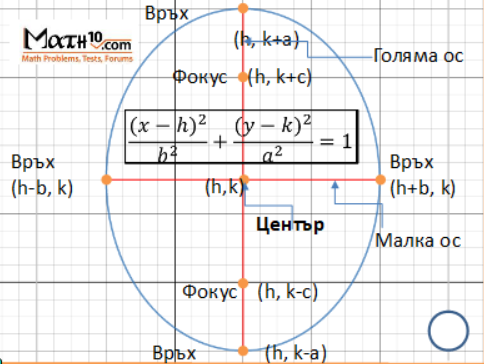
Знаем уравнението $\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ then
Върховете на големите оси са в точки $(h-a,k)\qquad (h+a,k)$ така
$V_{1}:(-4,0)\qquad V_{2}:(4,0)$
Върховете на малките оси са в точки $(h,k-b)\qquad (h,k+b)$ така
$CV_{1}:(0,-2)\qquad CV_{2}:(0,2)$
Ексцентрицитета $e=\frac{c}{a}=\frac{2\sqrt{3}}{4}\qquad e=\frac{\sqrt{3}}{2}$