Комплексни числа

Комплексното число (x, y) представлява двойка наредени реални числа - x и y.
Ако z = (x,y) - z е комплексно число,
x е реалната част z,а y се нарича имагинерна част на z.
Ако имаме две комплексни числа z1 = (x1, y1) и z2 = (x2, y2) то:
$z_1 = z_2 \Leftrightarrow x_1 = x_2$ and $y_1 = y_2$
$z_1 \pm z_2 = (x_1, y_1) \pm (x_2, y_2) = (x_1 \pm x_2, y_1 \pm y_2)$
$z_1z_2 = (x_1, y_1)\times (x_2, y_2) = (x_1x_2 - y_1y_2, x_1y_2 + y_1x_2)$
$\frac{z_1}{z_2}=\frac{(x_1, y_1)}{(x_2, y_2)}=\big(\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}, \frac{x_2y_1-x_1y_2}{x_2^2+y_2^2}\big)$
За всяко комплексно число (x, y) съществува съответна точка в координатната система. Не може да напишем, че
$A > B$, поради това не можем да напишем $(x_1, y_1) > (x_2, y_2)$, поради това комплексните числа нямат подредба.
Комплексните числа са от множеството $\mathbb{C}$.
Множеството на реалните числа е под множество на комплексните числа.
Реалните числа са от видa $(x, 0), \ \ x \in \mathbb{R}$
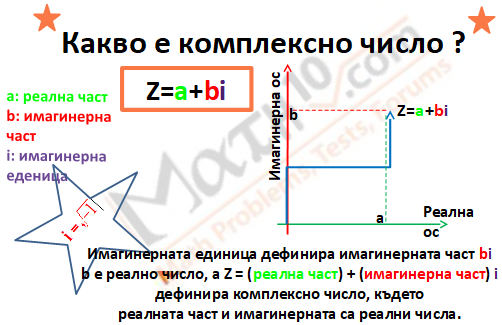
Друг начин да напишем z е: z = a + bi,
a е реалната част на z,
b е имагинерната част, а
i се нарича имагинерна единица $i^2 = -1, \ \ i = \sqrt{-1}$.
Всчко комплексно число $z = a + bi$ има негово комплексно спрегнато $\overline{z} = a - bi$.
- z + z = 2a - реално число;
- z - z = 2bi - имагинерно число;
- z.z = a2 + b2 = |z|2 - реално число
Действия с комплексни числа
сбор на две комплексни числа:
разлика на две комплексни числа:
умножение на две комплексни числа:

деление на две комплексни числа:
$\frac{a + bi}{c + di}=\frac{(ac + bd)+(bc - ad)i)}{c^2+d^2}$
| Правило | Стойност | Степен |
|---|---|---|
| $i^1 = i$ | $i^{4n + 1} = i$ | Кратни на 4 + 1 ${4n + 1, \ n \in \mathbb{Z}} = {1; 5; 9...}$ |
| $i^2 = -1$ | $i^{4n + 2} = -1$ | Кратни на 4 + 2 ${4n + 2, \ n \in \mathbb{Z}} = {2; 6; 10...}$ |
| $i^3 = -i$ | $i^{4n + 3} = -i$ | Кратни на 4 + 3 ${4n + 3, \ n \in \mathbb{Z}} = {3; 7; 11...}$ |
| $i^4 = 1$ | $i^{4n} = 1$ | Кратни на 4 ${4n, \ n \in \mathbb{Z}} = {4; 8; 12...}$ |
Тригонометричен вид
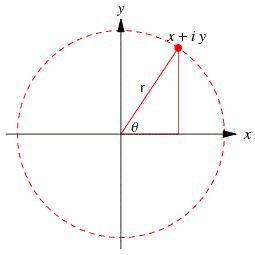
Тригонометричен вид на комплексното число е:
или
z = r(cos(θ) + i.sin(θ)) = r.ei.θ
|z| се нарича модул на комплексното число(то е равно на дължината на отсечката OM) θ се нарича аргумент на комплексното число. Кръга на картинката по-горе представя модула |z| на числото z и ъгъла θ - неговия аргумент.
Ако имаме 2 комплексни числа представени в тригонометричен вид:
z1 = r1(cos(θ1) + i.sin(θ1)) и
z2 = r2(cos(θ2) + i.sin(θ2))
z1.z2 = r1.r2[cos(θ1 + θ2) + i.sin(θ1 + θ2)]
$\frac{z_1}{z_2}=\frac{r_1}{r_2}[\cos(\theta_1-\theta_2)+i.\sin(\theta_1-\theta_2)]$
Формули на Моавър
Степенуване на комплексно число:
zn = rn(cos(nθ) + i.sin(nθ))
Коренуване на комплексно число:
$\sqrt[n]{z}=\sqrt[n]{r}(\cos(\frac{\theta+2k\pi}{n})+i.\sin(\frac{\theta+2k\pi}{n}))$
k = 0, 1, 2,..., n-1

 Меню
Меню