Елипса, парабола, хипербола

Елипса с ценитър $C(x_0 \textrm{ , } y_0)$ и главна ос успоредна на оста $x$

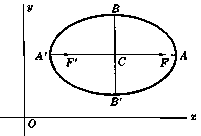
Дължина на главната ос $A'A = 2a$
Дължина на второстепенната ос $B'B = 2b$
Разтояние от центъра $C$ до фокуса $F$ или $F'$ е
$c = \sqrt{a^2 - b^2}$
Ексцентритет = $\epsilon = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a}$
Уравнение в ортонормирана координатна система:
$\frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1$
Уравнение в полярни координати ако $C$ съвпада с $O$:
$r^2 = \frac{a^2b^2}{a^2 \textrm{ sin }^2 \theta + b^2 \textrm{ cos }^2 \theta}$
Уравнение в полярна координатна система ако $C$ е върху оста $x$ и $F'$ съвпада с $O$:
$r = \frac{a(1 - c^2)}{1 - c \textrm{ cos } \theta}$
Ако $P$ е точка от елипсата, $PF + PF' = 2a$
Ако главната ос е успоредна на оста $y$, сменяйки $x$ и $y$ от по-горното и заменяйки θ с $\frac{1}{2}\pi - \theta$ [или $90^\circ - \theta$]

Парабола с оси успоредни на оста $x$

Ако върха е точка $A(x_0 \textrm{ , } y_0)$ и разтоянието от $A$ до фокуса $f$ е $a > 0$, уравнението на параболата е(ако параболата е отворена надясно)

$(y - y_0)^2 = 4a(x - x_0)$

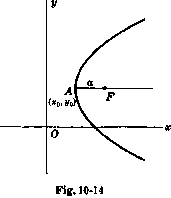
Ако параболата е отворена наляво
$(y - y_0)^2 = -4a(x - x_0)$

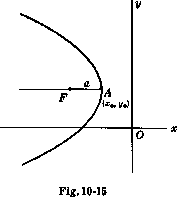
Ако фокуса съвпада с центъра на координатната система, уравнението в полярни координати е
$r = \frac{2a}{1 - \textrm{ cos } \theta}$



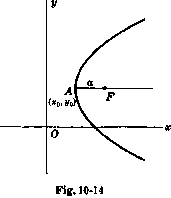
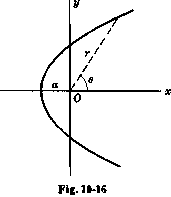
Ако оста е успоредна на оста $y$, разменяйки $x$ и $y$ или заменяне на $\theta$ с $\frac{1}{2}\pi - \theta$ [или $90^\circ - \theta$].

Парабола - анимация

Хипербола с център $C(x_0 \textrm{ , } y_0)$ и главна ос, успоредна на оста $x$

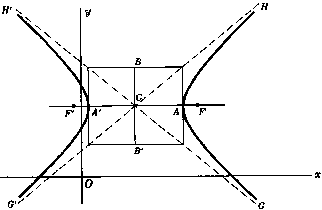
Дължина на главната ос $A'A = 2a$
Дължина на второстепенната ос $B'B = 2b$
Разтояние от центъра $C$ до фокуса $F$ или $F'$ е
$c = \sqrt{a^2 + b^2}$
Ексцентритет = $\epsilon = \frac{c}{a} = \frac{\sqrt{a^2 + b^2}}{a}$
Уравнение в правоъгълна координатна система:
$\frac{(x - x_0)^2}{a^2} - \frac{(y - y_0)^2}{b^2} = 1$
Наклони на асимптоти $G'H$ и $GH' = \pm \frac{b}{a}$
Уравнение в полярни координати ако $C$ съвпада с $O$:
$r^2 = \frac{a^2b^2}{b^2 \textrm{ cos }^2 \theta - a^2 \textrm{ sin }^2 \theta}$
Уравнение в полярни координати ако $C$ съвпада с оста $X$ и $F'$ съвпада с $O$:
$r = \frac{a(c^2 - 1)}{1 - \epsilon \textrm{ cos } \theta}$
Ако $P$ е точка от хиперболата, $PF - PF' = \pm 2a$ [в зависимост от клона]
Ако оста е успоредна на оста $y$, разменяйки $x$ и $y$ от по-горе $\theta$ с $\frac{1}{2}\pi - \theta$ [или $90^\circ - \theta$].

Анимация на хипербола