Множества

Множеството е основополагаща концепция в модерната математика, което означава, че самият термин няма дефиниция.
Въпреки това, множеството може да се представя като набор от различни елементи. Цялата модерна математика е основана на базата на тази концепция, следователно е важно да се знае и разбере теорията на множествата.
Множествата обикновено се представят с главните латински букви $A, B, C...$. Елементите на множеството са изписани в скоби $\lbrace$ и $\rbrace$.

Множествата могат да бъдат определени от:
1. Елементите си $A=\lbrace 1,2,3,4,5 \rbrace$
2. Правилата, на които се подчиняват елементите на множество. $A=\lbrace x\in \mathbb{N} \vert x<6\rbrace$

Множество без елементи се нарича празно множество и се представя чрез $\emptyset$ или $\lbrace \rbrace$.

Отношения между множествата

Равни множества

Две множества $A$ и $B$ са равни ако и само ако съдържат еднакви елементи. Ако елементите на първото множество са същите като на второто и обратното.

$A=B \overset{def}{\Leftrightarrow} (\forall x)(x\in A \Leftrightarrow x\in B)$

Подмножества

Множество $A$ е подмножество на $B$ ако и само, ако всеки елемент на $A$ е същевременно елемент и на множество $B$.

$A \subseteq B \overset{def}{\Leftrightarrow} (\forall x)(x \in A \Rightarrow x \in B)$

Множеството $B$ е надмножество на $A$,което е означено чрез $B \supseteq A$.
Ако множество $A$ е подмножество на $B$ и ако множеството $B$ съдържа поне един елемент, който не е принадлежи на множеството $A$, тогава казваме, че множеството $A$ е правилно подмножество на множество $B$, изразено чрез $A \subset B$, или, че множество $B$ е правилно надмножество на множество $A$, изразено чрез $B \supset A$.

Отношението $\subset$ е преходно: $(A \subset B) \wedge (B \subset C) \Rightarrow A \subset C$.

Празното множество е подмножество на всяко множество.

Действия с множества

Обединение на две множества

Обединяването на две множества, $A$ и $B$, е множество от всички елементи, които принадлежат на поне едно от множествата $A$ или $B$.

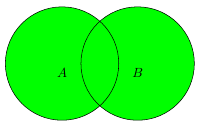
$A \cup B \overset{def}{=} \lbrace x \vert x \in A \vee x \in B \rbrace$

Операцията обединение на множества е:
1. $A\cup A=A$
2. Комутативно: $A \cup B = B \cup A$
3. Асоциативно: $(A \cup B) \cup C = A \cup (B \cup C)$

Сечение на множества

Сечението на две множества, $A$ и $B$, е множество съдържащо всички елементи, които принадлежат на двете множества $A$ и $B$.

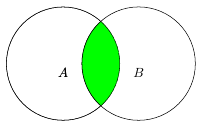
$A \cap B\overset{def}{=}\lbrace x \vert x\in A \wedge x\in B \rbrace$

Сечение на множества е:
1. $A\cap A=A$
2. Комутативно: $A \cap B = B \cap A$
3. Асоциативно: $(A \cap B) \cap C = A \cap (B \cap C)$

Разлика на множества

Разликата на две множества, $A$ и $B$, е множество съдържащо всичките елементи на множество $A$, които не принадлежат на множество $B$.

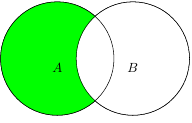
$A \setminus B \overset{def}{=} \lbrace x \vert x \in A \wedge x \notin B \rbrace$

Симетрична разлика

Симетричната разлика на две множества, $A$ и $B$, е множество съдържащо всичките елементи, които принадлежат само на едно от множествата $A$ и $B$.

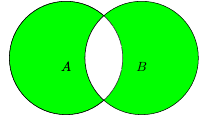
$A \bigtriangleup B \overset{def}{=} (A \setminus B) \cup (B \setminus A)$

Очевидно, че $\bigtriangleup$ е комутативно.

Допълнение на множество

Нека да приемем, че $A \subset B$. Допълнение на множеството $A$ по отношение на множество $B$ е множество съдържащо всички елементи на множество $B$, които не принадлежат на множество $A$.

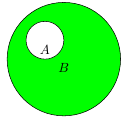
$C_B(A)\overset{def}{=}\lbrace x\vert x\in B \wedge x\notin A\rbrace$

Степен на множество

Степен на множество $A$ е множество от всички подмножества на $A$, включително празното множество и самото множество $A$.

$P(A) \overset{def}{=} \lbrace B \vert B \subset A \rbrace$

Пример: Степен на множество $A=\lbrace 1,2,3 \rbrace $ е множество $P(A)=\lbrace \emptyset ,\lbrace 1 \rbrace , \lbrace 2\rbrace, \lbrace 3 \rbrace , \lbrace 1,2 \rbrace , \lbrace 1,3 \rbrace , \lbrace 2,3 \rbrace , \lbrace 1,2,3 \rbrace \rbrace $

Декартово произведение

Декартово произведени на множествата $A$ и $B$ е множество съдържащо всички наредени двойки $(x,y)$ където $x$ е елемент на множество $A$, а $y$ елемент на множество $B$.

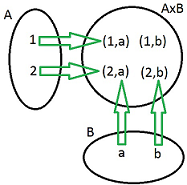
$A \times B \overset{def}{=} \lbrace(x,y) \vert x \in A \wedge y \in B \rbrace $

Действия с множества

Разпределение
$A \cup (B \cap C)=(A \cup B)\cap (A \cup B)$
$A \cap (B \cup C)=(A \cap B)\cup (A \cap B)$

Поглъщане
$A\cup(A\cap B)=A$
$A\cap(A\cup B)=A$

Закон на Де Морган
$C_U(A\cup B)=C_U(A)\cap C_U(B)$
$C_U(A\cap B)=C_U(A)\cup C_U(B)$

Отношения и функции

Отношения

Ако $A$ и $B$ са две непразни множества, тогава всяко подмножество $\rho$ на $A\times B$ се нарича бинарно отношение на множество $A\times B$.
Ако $(a,b)\in \rho$, казваме, че $a$ и $b$ са в отношение, и се изразяват чрез $a\rho b$.

Функции

Бинарно отношение $f\subset X\times Y$ се нарича функция тогава и само тогава, когато за всеки елемент $x\in X$ има съответстващ $y\in Y$ за което $(x,y)\in f$ е валидно, ако. $(\forall x\in X)(\exists !y\in Y)(x,y)\in f$

Изразени чрез символи: $f:X\longmapsto Y$ or $X\overset{f}{\longmapsto} Y$
Ако $(x,y)\in f$, пишем $f(x)=y$. Елемент $x$ се нарича оригинал, и $y$ изображение.
Множеството $X$ се нарича област, а множеството $Y$ съобласт на функцията $f$.
Три специални вида функции са от особено значение в математиката: инекция, сюрекция и биекция.

Инекция

Функция $f:X\longmapsto Y$ е инективна или "1-1" функция тогава и само тогава, когато за всеки елемент $x\in X$ има точно един елемент $y\in Y$, за който $f(x)=y$ е вярно.

$f:X\overset{1-1}{\longmapsto}Y\overset{def}{=}(\forall x_1,x_2\in X)(x_1\neq x_2\Rightarrow f(x_1)\neq f(x_2))$

Сюрекция

Функция $f:X\longmapsto Y$ е сюрективна или "върху" функция и само ако за всеки елемент $y\in Y$ има елемент $x\in X$ за който $f(x)=y$ е вярно.

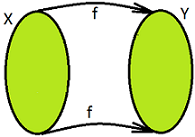
$f:X\overset{onto}{\longmapsto}Y\overset{def}{=}(\forall y\in Y)(\exists x\in X)(f(x)=y)$

Биекция

Функция $f:X\longmapsto Y$ е биективна, ако е едновременно инективна и сюрективна.