Формули от аналитичната геометрия в равнината

Разтояние $d$ между две точки $P_1(x_1 \textrm{ , } y_1)$ и $P_2(x_2 \textrm{ , } y_2)$

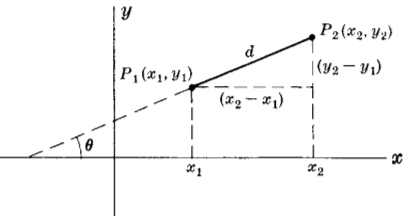
$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Наклон $m$ на права минаваща през 2 точки $P_1(x_1 \textrm{ , } y_1)$ и $P_2(x_2 \textrm{ , } y_2)$

$m = \frac{y_2 - y_1}{x_2 - x_1} = \textrm { tan } \theta$

Уравнение на права през две точки $P_1(x_1 \textrm{ , } y_1)$ и $P_2(x_2 \textrm{ , } y_2)$

$\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - y_1} = m$
или
$y - y_1 = m(x - x_1) \\ y = mx + b$

където $b = y_1 - mx_1 = \frac{x_2y_1 - x_1y_2}{x_2 - x_1}$ е секущата с $y$ оста, т.е. $y$ секуща.

Уравнение на права пресичаща осите $x \textrm{ , } y \qquad a \ne 0 \qquad b \ne 0$

$\frac{x}{a} + \frac{y}{b} = 1$

Нормално уравнение на права

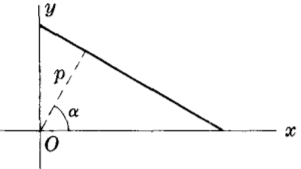
$x \textrm{ cos } \alpha + y \textrm{ sin } \alpha = p$
където $p$ = разтояние (перпендикуляр) от центъра $O$ до правата
и $\alpha$ = ъгъла между разтоянието от $O$ до правата с положителната страна на оста $x$.

Общо уравнение на права

$Ax + By + C = 0$

Разтояние между точка $(x_1 \textrm{ , } y_1)$ до права $Ax + By + C = 0$

$\frac{Ax_1 + By_1 + C}{\pm \sqrt{A^2 + B^2}}$
където знака е избран така, че разтоянието е положително число.

Ъгъл $\psi$ между две прави с наклон $m_1$ и $m_2$

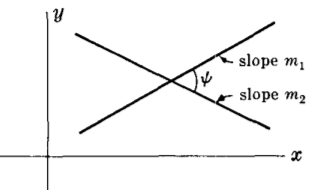
$\textrm{ tan } \psi = \frac{m_2 - m_1}{1 + m_1m_2}$
Правите са успоредни или съвпадащи, ако $m_1 = m_2.$
Правите са препендикулярни, ако $m_2 = -\frac{1}{m_1}.$

Лице на триъгълник с координати $(x_1 \textrm{ , } y_1) \textrm{ , } (x_2 \textrm{ , } y_2) \textrm{ , } (x_3 \textrm{ , } y_3)$

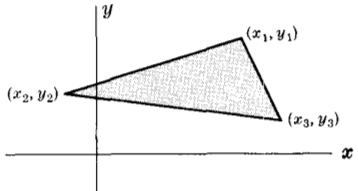
Лицето
$ = \pm \frac{1}{2} \left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right|$
$= \pm \frac{1}{2} ( x_1y_2 + x_2y_3 + x_3y_1 - x_1y_3 - x_2y_1 - x_3y_2 )$
където знакът така се избира, че лицето да не е отрицателно число. Ако лицето е нула, точките лежат на една права.

Още аналитична геометрия във форума