Основни диференциални уравнения и решенеията им

Уравнения с разделящи се променливи
f₁(x)g₁(y)dx + f₂(x)g₂(y)dy = 0

Решение
$\int\frac{f_1(x)}{f_2(x)}dx + \int\frac{g_2(y)}{g_1(y)}dy = c$

Линейно уравнение от първи ред
dx/dy + P(x)y = Q(x)

Решение
$y e^{\int P dx} = \int Q e^{\int P dx} dx + c$

Уравнение на Бернули
dy/dx + P(x)y = Q(x)yⁿ

Решение
$v e^{(1-n) \int P dx} = (1-n) \int Q e^{(1-n) \int P dx} dx + c$
където v = y^1-n.
Ако n = 1, решението е
$ln y = \int (Q - P ) dx + c$

Уравнение с точен диференциал
M(x,y)dx + N(x,y)dy = 0, където ∂M/∂y = ∂N/∂x.

Решение
$\int M \partial x + \int (N - \frac{\partial}{\partial y}\int M \partial x) dy = c$
където ∂x показва, че ще интегрираме по х, а у ще е константа.

Хомогенно уравнение
dy/dx = F(y/x).

Решение
$ln x = \int \frac{dv}{F(v) - v} + c$където v = y/x.Ако F(v) = v, решението е y = cx.

yF(xy)dx + xG(xy)dy = 0

Решение
$ln x = \int \frac{G(v) dv}{v \{G(v) - F(v)\} } + c$
където v = xy. Ако G(v) = F(v), решението е xy = c.

Линейно хомогенно уравнение от втори ред
d²y/dx² + a(dy/dx) + by = 0 , a,b са реални константи.

Решение
Нека m₁, m₂ са корени на m² + am + b = 0.Тогава има три слачая..

Случай 1.     m₁,m₂ реални и различни:
$y = c_1 e^{m_1 x} + c_2 e^{m_2 x}$

Случай 2.     m₁,m₂ реални и равни:
$y = c_1 e^{m_1 x} + c_2 x e^{m_1 x}$

Случай 3.     m₁ = p + qi,m₂ = p - qi:
$y = e^{px} (c_1 \cos qx + c_2 \sin qx)$

Линейно нехомогенно уравнение от втори ред
d²y/dx² + a(dy/dx) + by = R(x) , a,b са реални константи.

Решение
Има три случая аналогични на горните.

Случай 1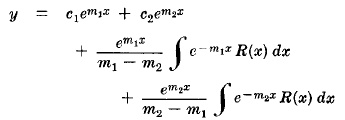

Случай 2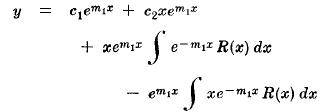

Случай 3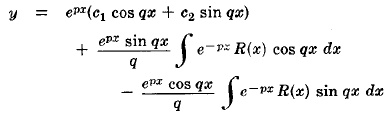

Уравнение на Ойлер или Коши
x²d²y/dx² + a(dy/dx) + by = S(x) .

Решение
Полагайки x = e^t, уравнението се превръща в
d²y/dt² + (a - 1)(dy/dt) + by = S(e^t)
и може да се реши като горните две.

Уравнение на Бесел
x²d²y/dx² + x(dy/dx) + (λ²x² - n²)y = 0.

Решение
y = c₁J_n(λx) + c₂Y_n(x).

Трансформирано уравнение на Бесел
x²d²y/dx² + (2p + 1)x(dy/dx) + (α²x^2r + β²)y = 0.

Решение
$y = x^{-p} \{c_1 J_{q/r} (\frac{\alpha}{\gamma}x^r) + c_2 Y_{q/r} (\frac{\alpha}{\gamma}x^r)\}$

където q = √p² - β².

Уравнение на Льожандър
(1 - x²)d²y/dx² - 2xdy/dx + n(n + 1)y = 0.

Решение
y = c₁P_n(x) + c₂Q_n(y).

Видео

от Любомир Андреев

Въведение в диференциалните уравнения

Уравнения с разделящи се променливи