Специални равнинни криви
Лемниската
Уравнение в полярни координати:
$r^2=a^2\cos2\theta$
Нормално равнение:
$(x^2+y^2)^2=a^2(x^2-y^2)$
Ъгъл между $AB'$ или $A'B$ и оста $x = 45^\circ$
Уравнение на затворена крива $=\frac{a^2}{2}$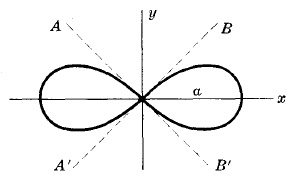
Циклоид
Уравнения в параметрична форма: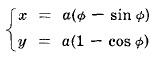
Уравнение на една арка = 3πa2
Дължина на арка = 8a
Това е прива описана от точка P по кръг с радиус a движеща се по оста х.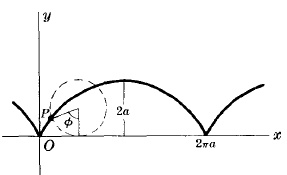
Хипоциклоид с четири листа
Уравнение в квадратни координати:
$x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3}$
Параметрично уравнение:
$\left\{\begin{array}{lr}x=a\cos^3\theta\\ y=a\sin^3\theta\end{array}\right.$
Лицето на хиперболоид ограден от крива е $\frac{3\pi a^2}{8}$
Дължина на цялата крива е $6a$
Tова е крива описана от точка $P$ по окръжност с радиус $\frac{a}{4}$ като се движи по вътрешността на окръжност с радиус $а$.
Кардиоид
Уравнение: $r=a(1+\cos\theta)$
Лицето на кардиоид ограден от крива е $\frac{3\pi a^2}{2}$
Дължина на крива е $8a$
Това е кривата описана от точка Р по окръжност с радиус а като се движи по външността на фиксирана окръжност с радиус a. Кривата също е специален случай на limacon of Pascal.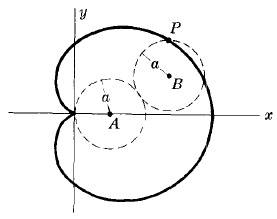
Дъга
Уравнение:
y = a(ex/a + e-x/a)/2 = acosh(x/a)
Това е крива, на която ако е окачена тежка верига вертикално от фиксирани точки А и В ще виси.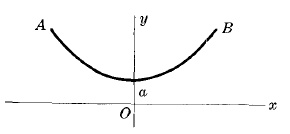
Трилистна роза
Уравнение: r = acos3θ
Уравнението r = acos3θ е подобна на крива получена чрез въртене на кривата по посока обратна на часовниковата стрелка на 30o или π/6 радиани.
По принцип r = acosnθ или r = asinnθ има n листа ако n е нечетно.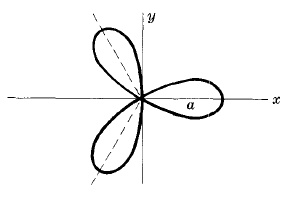
Четирилистна роза
Уравнение: r = acos2θ
Уравнението r = asin2θ е подобна крива получена чрез въртене на кривата по посока обратна на часовниковата стрелка на 45o или π/4 радиани.
По принцип r = acosnθ или r = asinnθ има 2n листа ако n е четно.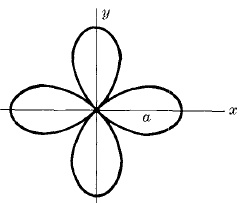
Епициклоид
Полярни уравнения: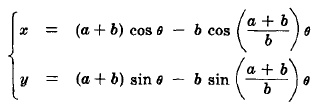
Това е крива описана от точка P от окръжност с радиус b като се движи по външаната страна на окръжност с радиус а.Кардиоида е частен случай на епициклоид.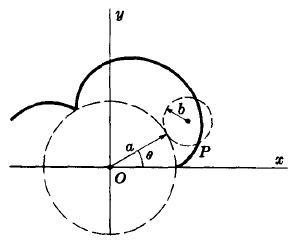
Обикновен хипоцикоид
Полярни уравнения: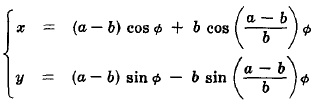
Това е крива описана от точка Р от кръг с радиус b като се движи по външността на окръжност с радиус а.
Ако b = a/4, кривата е хипоциклоид с четири листенца.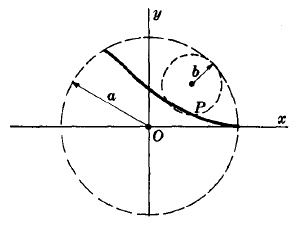
TROCHOID
Полярни уравнения: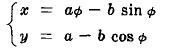
Това е крива описана от точка P на разстояние b от центъра на окръжност с радиус a като окръжността се движи по оста х.
Ако b < a, кривата е показана на Fig.11-10 и се нарича curtate циклоид.
Ако b > a, кривата е показана на Fig.11-11 и се нарича prolate циклоид.
Ако b = a, кривата е циклоид.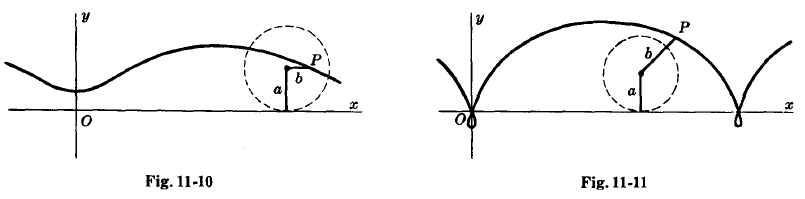
TRACTRIX
Полярни уравнения: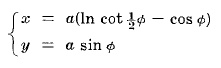
Това е крива описана от външна точка P на права отсечка PQ с дължина a като другия край Q се мести по оста х.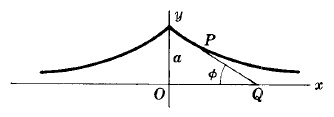
WHITCH OF AGNESI
Уравнение в квадратни координати: y = 8a3/(x2 + 4a2)
Параметрични уравнения: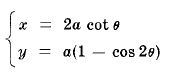
На фигурата променящата се права OA пресича y = 2a и окръжността с радиус a с център (0,a) в A и B съответно. Всяка точка P "която" се разполага чрез спускане на прави успоредни на осите x и y през точките B и съответно A и се определя точката P на пресичане.
Фолио на Декарт
Уравнение в квадратни координати:
x3 + y3 = 3axy
Параметрични уравнения: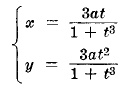
Уравнение с наклон 3a2/2
Уравнение на асимптота: x + y + a = 0.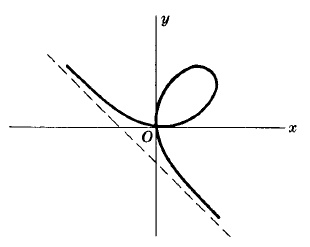
СПИРАЛА на кръг
Параметрични уравнения: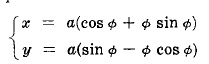
ТОва е крива описана чрез крайната точка P на нишка, която се развива от окръжност с радиус a докато стане права.
EVOLUTE на елипса
Уравнение в квадратни координати:
(ax)2/3 + (by)2/3 = (a2 - b2)2/3
Параметрични уравнения: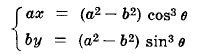
Това е крива на envelope на нормалите на елипсата x2/a2 + y2/b2 = 1.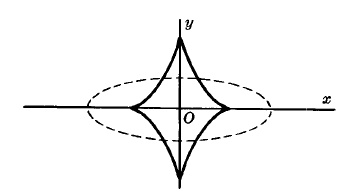
Овали на Касини
Полярно уравнение: r4 + a4 - 2a2r2cos2θ = b4.
Това е крива описана от точка P така че накрая разстоянието от две фиксирани точки[разстоянието 2а] е константата b2.
Кривата е на фигурите съответно когато b < a или b > a.
Ако b = a, кривата е lemniscate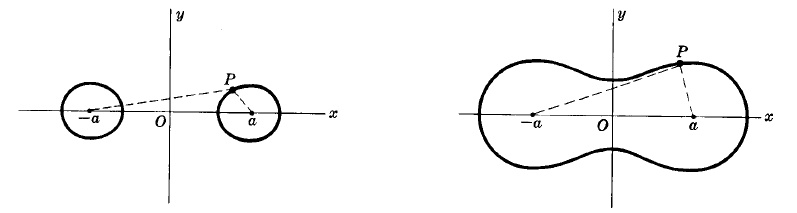
LIMASCON на Паскал
Полярно уравнение: r = b + acosθ
Нека OQ е права свързваща началото О, с която и да е точка Q от окръжностс диаметър a минаваща през О.Тогава кривата е множеството на всички точки Р така че PQ = b.
Кривата е като на фигурите по-долу сътветно когато b > a или съответно b < a. Ако b = a, кривата е кардиоид.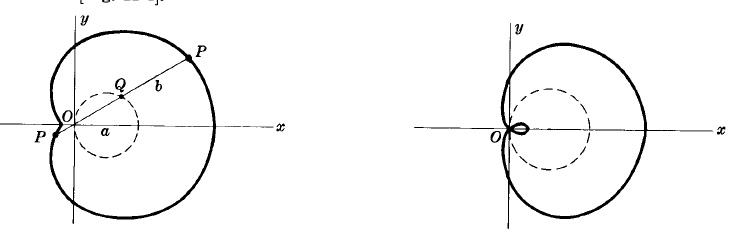
CISSOID на Диоклес
Уравнение в квадратни координати: y2 = x3/(2a - x)
Параметрични уравнения: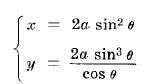
Това е крива описана от точка Р така, че разстоянието ОР = разстоянието RS. Използвано е при проблема с дупликиране на куб, т.е. намиране на страната на куб, който има два пъти по-голям обем от даден куб.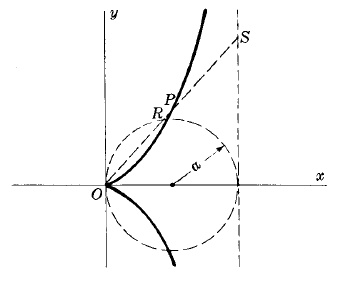
Спирала на Архимед
Полярно уравнение: r = aθ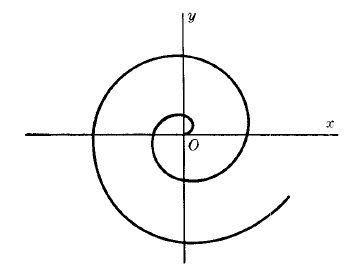

 Меню
Меню