Примерна тема №1 за кандидат-студентски изпит

Темата за изпита по математика е взета от сайта на ПМГ-Стара Загора.

Задача 1. Да се реши уравнението
log₂(2^{x - 1} + 3^{x + 1}) = 2x - log₂3^x.

Задача 2. В триъгълник АВС < ACB = 120°. Точката D лежи върху отсечката АВ и АD = 1, ВD = 6, СD = 2. Да се намерят страните АС и ВС на триъгълника АВС.

Задача 3. Да се намери обемът на правилна триъгълна пирамида, ако големината на ъгъла между две околни стени е равен на 2а, а разстоянието от центъра на основата на пирамидата до околна стена е равно на р.

Задача 4. Нека f(х) = ах² + bх + с, където а, b и с са реални числа. Да се докаже, че:
а) f(x) = ( x(x - 1)f(-1)/2) + (1 - x²)f(0) + ( x(x + 1)f(1) )/2;
б) ако |f(-1)| ≤ 1; |f(0)| ≤ 1 и |f(1)| ≤ 1, то |f(x)| ≤ 5/4 за всяко x [-1, 1].

Решения на задачите от тренировъчна тема №1

1.Задача:   Уравнението има смисъл за всяко х и е еквивалентно на показателното уравнение 6.3^2х + 2^x.3^x — 2.2^2x = 0. Полагаме t = (3/2)^x и получаваме 6t² + t - 2 = 0, откъдето t = 1/2 или t = —2/3. Уравнението (3/2)^х = -2/3 няма реални корени, а от (3/2)^х = 1/2 получаваме х = log_3/2 1/2 = 1/(1 - log₂ 3).

2.Задача:   Нека 2 = 5 - 4cosφ и а² = 40 + 24cosφ. Оттук следва, че а² + 6b² = 70. Пак от косинусовата теорема за ΔАВС намираме, че а² + b² + аb = 49. Получената система за а и b е хомогенна и има единствено решение а = √7, b = 2√7

3.Задача:   Нека пирамидата е АBCD, с основа ΔАВС, основен ръб AB = а и височина DO = h (черт. 1).

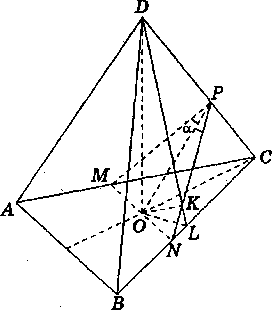
Нека равнината през 0, перпендикулярна на СD пресича (АВС) в права МN, а СD в т.Р. Тогава МN||AB(докажете!), NP, то ОК(BCD) (защо?) и значи OK = p. Имаме, че V = (1/12)a²√3h. От ΔPON намираме MN = 2p/cosα. Но MN = (2/3)a. Следователно a = 3p/cosα. От друга страна, тъй като BC(DOK), то DK∩BC = L, където L е средата на BC(черт. 1). Тогава от ΔDOL имаме, че 2S_DOL = h.OL = p.DL = p.√h² + OL², откъдето h = (p.OL)/√OL² - p². Но OL = (a.√3)/6 = (p√3) /2cosα. Следователно h = (p√3)/(√3 - 4cos²α и V = 9p³/(4cos²α√3 - 4cos²α). Задачата има смисъл ако 3 - 4cos²α > 0(т.е. OL > p), което е изпълнено за α (π/6; π/2).