Задачи за първи признак за еднаквост на триъгъглници

Задача 1
Даден е триъгълник АВС – равнобедрен, СD е ъглополовяща към основата АВ . Да се докаже, че триъгълник АСD е еднакъв на триъгълник ВСD

Задача 2
Докажете, че височината,ъглополовящата и медианата прекарани към основата на равнобедрен триъгълник съвпадат.
Решение:
От предходната задача имаме че СD е ъглополовяща в равнобедрения триъгълник АВС и доказахме, че триъгълник АСD е еднакъв на триъгълник ВСD. От еднаквостта следва че ъгъл АDС = СDВ, но те са съседни следователно сборът им е 180°, откъдето следва ъгъл АDС = СDВ = 90°, което показва, че СD е и височина. От еднаквостта на двата триъгълника имаме страната АD = ВD, т.е. СD е и медиана.

Задача 3
Докажете, че ъглите при основата на всеки равнобедрен триъгълник са равни.
Решение:
Отново използуваме зад. 1 и това че триъгълник АСD и триъгълник ВСD са еднакви. Ъглите при основата на равнобедрения триъгълник са равни защото са съответни ъгли в еднакви триъгълници.

Задача 4
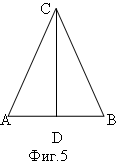
Пресметнете периметърът на равнобедреният триъгълник АВС, ако периметърът на >АDС е 18 см., а СD = 6 см. и АD = ВD (фиг.5)
Решение:
Периметърът на триъгълник АDС = АС+ СD + АD = 18 <=> АС + 6 + AD = 18 <=> AC + AD = 12
Понеже АС = ВС (триъгълника е равнобедрен) и АD = DВ то АС + АD = DВ +ВС = 12
Периметърът на триъгълник АВС = АВ + АС + ВС = АD + DВ + АС + ВС = 12 + 12 = 24см.

Задача 5
Докажете, че права която отсича равни отсечки от раменете на даден ъгъл, е перпендикулярна на ъглополовящата на този ъгъл.
Решение:

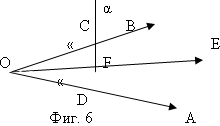
Нека правата отсича от раменете на ъгъл АОВ равни отсечки ОС = ОD . Тогава триъгълник ОСD е равнобедрен и ОF е ъглополовяща към основата му. Съгласно зад.2 ОF е и височина, т.е. ОF е перпендикулярна на α

Задача 6
Докажете, че ако диагоналите на един четириъгълник взаимно се разполовяват, то всеки две от срещу лежащите му страни са равни.
Решение:

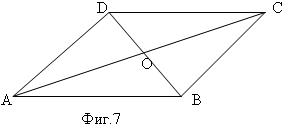
За четириъгълника АВСD е известно, че АО = ОС и ВО = ОD Тогава триъгълник АОD и триъгълник ВОС са еднакви (І признак, АО = ОС; ВО = ОD и ъглите DОА = ВОС – връхни) следователно АD = ВС Аналогично се доказва, че триъгълник АОВ и триъгълник DОС са еднакви, откъдето следва, че АВ = СD

Задача 7
Докажете, че ако триъгълник АВС е еднакъв на А₁В₁С₁ и за точките М и М₁ от страните АВ и А₁В₁ съответно е в сила АМ = А₁М₁, то СМ = С₁М₁ и ъгъл ВМС = В₁М₁С₁
Решение:

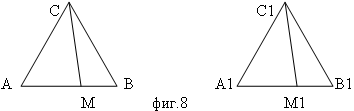
Понеже триъгълник АВС е еднакъв на триъгълник А₁В₁С₁, то АВ = А₁В₁, ВС = В₁С₁, СА = С₁А₁ и ъглите А = А₁, В = В₁, С = С₁. Тогава триъгълник АМС е еднакъв на А₁М₁С₁ (І признак), защото АС = А₁С₁, АМ = А₁М₁ и ъгъл А = А₁, откъдето следва, че СМ = С₁М₁. Твърдението МВ = М₁В₁ следва от това, че те се получават от равните отсечки АВ и А₁В₁, като се извадят равните отсечки АМ и А₁М₁. Ъглите ВМС и В₁М₁С₁ са равни защото те са съседни ъгли съответно на ъглите АМС и А₁М₁С₁, които са равни (триъгълник АМС е еднакъв на триъгълник А₁М₁С₁)

Задача 8
Даден е триъгълник АВС (АС < ВС). Външно за него са построени:
квадратите ВМNC и CPQA. Да се докаже, че АN = ВР

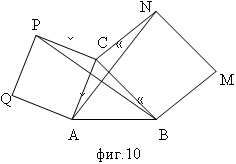
Решение:
Разглеждаме триъгълниците ВРС и АСN, за които ВС = СN (ВМNC – квадрат);
PC = AC (CPQA - квадрат) ъгъл ВСР = АСN = 90° + АСВ. Следователно по І признак двата триъгълника са еднакви от където следва, че АN = ВР

Още за еднакви триъгълници във форума

Форум за триъгълници

Още триъгълни във форума за математика