Сбор на вектори

Нека са дадени вевкторите , , , (черт.3). Да построим с начало произволна точка O вектор = ,
след това с начало A – вектор = ,
с начало B – вектор =
и с начало C – вектор = .

Векторът с начало – началото O на първия вектор и с край – края D на последния(в случая – четвъртия) вектор и всеки равен на него вектор се нарича сбор (резултанта) на векторите , , , , а последните – негови събераеми(компоненти). Извършеното бележим

= + + + = + + +

От чертежа се вижда, че до същата резултанта ще стигнем и в случая, когато изберем друга точка O' за начало, както и ако променим реда на събераемите(комутативен закон).

Така, на чертежа е сменен редът на втората и третата събераеми, но резултантата е останала същата, тъй като от успоредника АВ₁СВ следва, че = и = . Ако краят F на последния събераем вектор съвпадне с началото A на първия, резултантата е нулев вектор, т.е.
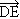+ + + + = = = 0

Разлика на два вектора

Нека и са вектори. Търсим вектор , такъв, че да имаме
+ =

Векторът и всеки равен на него вектор се нарича разлика на векторите и , което бележим = -

Разликата на векторите и построяваме, като построим с общо начало О векторите = и =

Векторът има желаното свойство, тъй като, съгласно определението за сбор на вектори, имаме + = или
+ = . Разликата можем да построим и като сбор на векторите и -, противоположен на

Теорема. 1:

Теорема 2.

Още за вектори във форума

Форум за вектори

Още вектор във форума за математика