Равенство на вектори

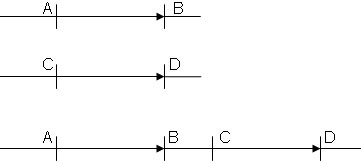
Два вектора и са равни, когато и двата са нулеви или и двата са ненулеви, но са еднопосочни и имат равни дължини. Директрисите на равни вектори са успоредни или се сливат. Равенството на два вектора бележим =

Често се използва следният признак за равенство на вектори:
Векторите и , нележащи върху една и съща права, са равни, ако четириъгълникът АВСD е успоредник. Оттук следва, че ако = , то =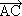

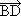
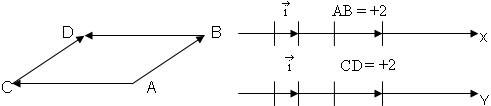
Два севгмента върху еднопосочни(успоредни или сливащи се) оси с равни единични сегменти са равни помежду си, ако имат равни релативни мерки и обратно.

От определението за равни вектори следват свойствата

1. Всеки вектор е равен на себе си, т.е. =
2. Ако = , то =
3. Ако = , то = , то =

Още за вектори във форума

Форум за вектори

Още вектор във форума за математика