Забележителните точки в триъгълник

Автор: Андон Илиянов Андонов

Забележителните точки в триъгълник са: медицентърът G; центърът на вписаната окръжност J; центърът на описаната окръжност O; ортоцентърът H и центровете на външновписаните окръжности J₁, J₂, J₃.

Медицентърът G е пресечна точка на трите медиани в един триъгълник.

T: Ако ABC е с медиани AA₁, BB₁ и CC₁ и медицентър G, то AG/GA₁ = BG/GB₁ = CG/GC₁ = 2/1.

Ортоцентърът H е пресечната точка на трите височини в един триъгълник.

Основна задача: Ако ABC е с височини AH₁, BH₂, CH₁ и ортоцентър H, BAC = α, ABC = β, ACB = φ, то: CH₁H₂ = α, CH₂H₁ = β, BH₃H₁ = φ, BH₁H₃ = α, AH₂H₃ = β, AH₃H₂ = φ.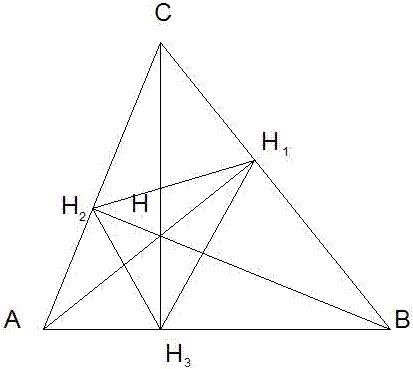

Доказателство:
Разглеждаме четириъгълника ABH₁H₂ : AB се вижда под ъгъл 90^o от точки H₁ и H₂ около ABH₁H₂ може да се опише окръжност.
         ⇒ BH₁H₂ = 180^o - α ⇒ CH₁H₂ = α;
                AH₂H₁ = 180^o - β ⇒CH₂H₁ = β;

Аналогично се доказва и за ъглите α и φ.

* * *

Центърът на вписаната окръжност J е пресечната точка на трите ъглополовящи в триъгълника.

Центърът на описаната окръжност O е пресечната точка на трите симетрали на страните на триъгълника.

Центърът J_a на външновписаната окръжност е пресечна точка на ъглополовящата на BAC и външните ъгли при върховете B и C. Тази окръжност се допира до страната BC и продълженията на другите две.
      Аналогично е и за J_b и J_c.

Точките M и J са винаги вътрешни за триъгълника, защото трите медиани и трите ъглополовящи по определение лежат вътре в триъгълника. Точките O и H са вътрешни за остроъгълния триъгълник, лежат на страна или връх в правоъгълния и са външни за тъпоъгълния.

Центърът на описаната окръжност О е пресечната точка на трите симетрали на страните на триъгълник.Трите точки заедно (H,O,G) образуват права на Ойлер.

Т: във всеки ABC ортоцентърът, центърът на описаната окръжност и медицентърът лежат на една права.

Доказателство:

Нека O и H са съответно центърът на описаната окръжност и ортоцентърът на триъгълника. Ако триъгълникът е равнобедрен, H съвпада с O, а ако е правоъгълен, H съвпада с C, т.е. в тези случаи твърдението е вярно. Нека триъгълникът ABC е разностранен и остроъгълен. Тогава О ≠ H. Тези две точки определят права, която пресича медианата CS в точка G. Ще докажем, че G е медицентърът на ?ABC, откъдето ще следва твърдението.Да означим с F и L съответно средите на GH и GC. Тогава FL е средна отсечка в GHC, т.е. CH=2*LF и CH || LF. Но 2*OS = CH и OS || CH ( доказано в Задача 6 ). Следователно SO = LF и SO || LF, т.е. SFLO е успоредник. Тогава GS = GL ( диагоналите в успоредника взаимно се разполовяват). Следователно CG : GS = 2 : 1, т.е. G е медицентърът на ABC.

Триъгълникът, който се образува от петите на перпендикулярите на трите височини, се нарича ортотриъгълник. Ще докажем някои свойства на този триъгълник чрез следващите задачи.

Задачи:

Задача 1:
    Точка H е центърът на вписаната окръжност в триъгълник H₁H₂H₃.

Доказателство:
В горепосочената основна задача установихме, че ако ABC е с височини AH₁, BH₂, CH₃ и ортоцентър H, BAC = α, ABC = β, ACB = φ, то: CH₁H₂ = α, CH₂H₁ = β, BH₃H₁ = φ, BH₁H₃ = α, AH₂H₃ = β, AH₃H₂ = φ. Като се използват равенствата, не е трудно да се докаже, че HH₃H₂ = HH₃H₁ = 90^o - β. ⇒ H₃C е ъглополовяща на H₂H₃H₁. Аналогично доказваме, че H₁A и H₃B са ъглополовящите на H₃H₁H₂ и H₁H₂H₃. ⇒ H е центърът на вписаната в триъгълник H₁H₂H₃ окръжност.

Задача 2:
Върховете на ABC са центрове на външновписаните за H₁H₂H₃ окръжности.

Доказателство:
Нека D е точка от правата H₃H₁ като H₁ е между H₃ и D.
    Лесно се доказва, че CH₁D = H₃H₁B. Tогава, като имаме предвид равенствата, получаваме, че H₁C е ъглополовяща на H₂H₁D, който е външен ъгъл за H₁H₂H₃. В 1) установихме, че H₃C е ъглополовяща на H₂H₃H₁. Точка А е пресечна точка на тези две ъглополовящи. Следователно тя е център на външновписаната за H₁H₂H₃ окръжност, която се допира до страната H₁H₂. По същия начин се установява, че точките B и C са центрове на другите също външновписани окръжности за H₁H₂H₃.
    да отбележим, че ако триъгълникът е тъпоъгълен, тогава ортоцентърът и върховете на острите му ъгли са центрове на външновписаните окръжности за H₁H₂H₃.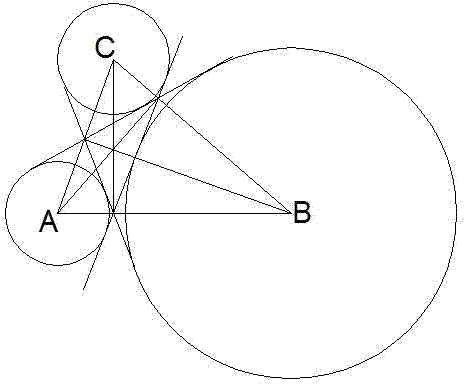

След като доказахме някои от свойствата на ортотриъгълника, ще изложим някои други задачи, в които ще покажем свързващи свойства на забележителните точки в триъгълник.

Задача 3:
    Даден е остроъгълен триъгълник ABC с ACB = 60^o. Докажете, че центърът на описаната окръжност, ортоцентърът и върховете A и B лежат на една окръжност с център пресечната точка на ъглополовящата през върха C и симетралата на страната AB.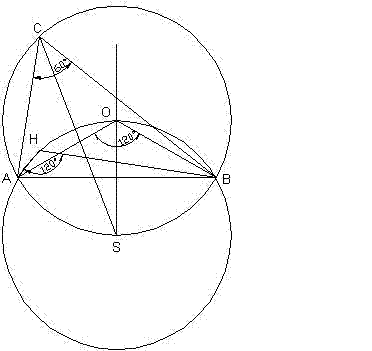

Доказателство:
    Построяваме окръжност с център S (ъглополовящата на ъгъл C пресича S_AB в точка S) и радиус SB = SA ⇒ А и B лежат на окръжността. ACB – вписан в K, и ACB = 60^o. AOB – централен ъгъл ⇒ AOB = 2.ACB = 120^o.SO - S_AB ⇒ AOS = BOS = 60^o. AB OS и AB разполовява OS ⇒ триъгълник ASO е равностранен ⇒ OA = OS ⇒ O лежи на K¹.H – ортоцентър ⇒ AHB = 180^o - ACB = 180^o - 60^o = 120^o. AOB = AHB ⇒ A,O,H и B лежат на една окръжност с център пресечната точка на S_AB и ъглополовящата на ACB.

Задача 4:Даден е остроъгълен триъгълник ABC с ортоцентър H, център на вписаната окръжност J и център на описаната окръжност O. Намерете ACB, ако:
    а) точките A,O,J и B лежат на една окръжност;
    б)точките A,H,J и B лежат на една окръжност.

Решение :
a)    Щом A,O,J и B лежат на една окръжност,
то AJB = AOB. Ако ACB = γ,
то AOB = 2γ (централен ъгъл).
AJB = 2γ. Щом AJB = 2γ
180^o - (α + β)/2 = 2γ. Но α + β = 180^o - γ
180^o - (90^o - γ/2) = 2γ.
90^o = 3γ/2
⇒ γ = 60^o.

б)
    Отново нека ACB = γ. Лесно се доказва, че AHB = 180^o - γ. Понеже точките A,H,J и B лежат на една окръжност, следва, че AHB = AJB.
AJB = 180^o - γ;
180^o - (α + β)/2 = 180^o - γ;
2γ = α + β;
2γ = 180^o - γ;
γ = 60^o;

Задача 5:
    В триъгълник ABC ъглополовящите AA₁ и BB₁ се пресичат в точка J, а O е центърът на описаната около триъгълника окръжност. Да се докаже, че точките J, A₁,C и b₁ лежат на една окръжност тогава и само тогава, когато точките J, A, O и B лежат на една окръжност.

Доказателство:
I случай: Ще докажем, че ако J, A₁, C и B₁ лежат на една окръжност, то точките J, A, O и B лежат на една окръжност.
⇒ A₁JB₁ = 180^o - γ.
Тъй като A₁JB₁ = AJB,
от това следва, че 180^o - (α + β)/2 = 180^o - γ;
Но α + β = 180^o - γ
90^o - γ/2 = γ;
γ = 60^o;
AJB = 120^o;
Но AOB е централен ъгъл:
⇒ AOB = 2.ACB = 2*60^o = 120^o;
⇒ AOB = AJB = 120^o;
⇒ точките J,A,O и B лежат на една окръжност.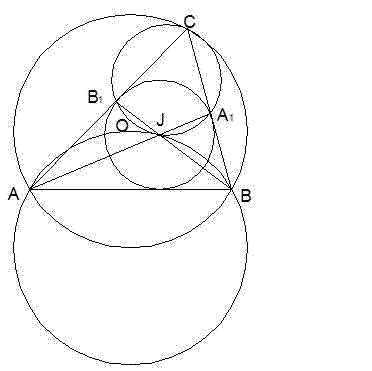

II случай:
    Ще докажем, че ако точките J,A,O и B лежат на една окръжност, то J, A₁, C и B₁ също лежат на една окръжност.
AOB е централен ъгъл
⇒ AOB = 2γ;
J е център на вписаната окръжност,
AJB = 180^o - (α + β)/2;
Но J,A,O и B лежат на една окръжност
⇒ AOB = AJB;
180^o - (α + β)/2 = 2γ;
Но α + β = 180^o - γ;
⇒ 180^o -90^o - γ/2 = 2γ;
3γ/2 = 90^o;
γ = 60^o;
⇒ AOB = 120^o = AJB;
Но AJB = A₁JB₁;
A₁JB₁ = 120^o;
A₁JB₁ = 180^o - γ;
⇒ J, A₁, C и B₁ също лежат на една окръжност;

Задача 6:
    Докажете, че в триъгълник разстоянието от ортоцентъра до връх на триъгълника е два пъти по-голямо от разстоянието от центъра на описаната окръжност до срещулежащата на този връх страна.

Доказателство:
    Ще докажем, че AH = 2.OM. Построяваме правата BO.BO пресечено с K = B₁.⇒ BB₁ - диаметър.⇒ B₁BC и ABB₁ са вписани в полуокръжност. ABB₁ = BCB₁ = 90^o. Разглеждаме четириъгълника AHCB₁ . CH – височина ⇒ CH AB; B₁A AB ⇒ CH и АB₁ са успоредни (1). AH – височина и B₁CB = 90^o ⇒ AH и B₁ C са успоредни (2). От (1) и (2) ⇒ AHCB₁ е успоредник. ⇒ AH = B₁C. BB₁ - диаметър ⇒ BO = ОB₁ (3); OM BC (4);
От (3) и (4) ⇒ OM – средна отсечка в BCB₁. 2.MO = B₁C. Но B₁C = AH
⇒ 2.MO = AH. Аналогично и за останалите ъгли и срещулежащите им страни.

Задача 7:
    Oтсечките AM и BN са височини в остроъгълния триъгълник ABC, а точка O е център на описаната около триъгълника окръжност. Да се докаже, че радиусът OC е перпендикулярен на отсечката MN.

Доказателство:
    Отсечката AB се вижда от точките M и N под прав ъгъл.Следователно M и N лежат на окръжност с диаметър AB. Като използваме свойствата на вписаните ъгли, получаваме следните равенства:
CNM = AМ/2 = ABC, OCN + ABC = AP/2 (CO пресича окръжността описана около ABMN в т.P) + AC/2 = 90^o
⇒ NM OC.

Задача 8:
    Даден е остроъгълен триъгълник ABC с височини AD, BE и CF и ортоцентър H.
а) Да се докаже, че H може да разполовява най-много една от височините;
б) Ако CH = HF и AH : HD = 1 : 3, да се докаже, че триъгълникът ABC е равнобедрен и BD : DC = 2 : 1.

Решение :
а)Допускаме, че H разполовява поне две от височините, например CH = HM и AH = HN. Отсечките AN и CM се разполовяват от пресечната си точка, следователно четириъгълникът AMNC е успоредник и AM || CN . Но тези прави се пресичат в точка B. Получава се противоречие, което показва, че H може да разполовява най-много една от височините.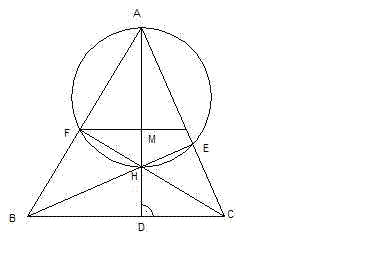

б)Върху AH нанасяме HM = HD. От даденото по условие равенство AH : HD = 3 : 1 следва, че M е среда на AD. Диагоналите на четириъгълника MFDC взаимно се разполовяват, следователно той е успоредник, т.е. CD = MF и MF || BC. От това и от факта, че M е среда на AD, следва, че MF е средна отсечка в ABD. Следователно BC : CD = BD : MF = 2 : 1 и F е среда на AB, т.е. ABC е равнобедрен.

Задача 9:    Около триъгълника ABC е описана окръжност. Нека A₁, B₁ и C₁ са среди съответно на дъгите BC, CA и AB(BC ∉ A, CA ∉ B, AB ∉ C). Хордата A₁C₁ пресича AB в точка P и BC в точка Q. Хордата B₁C₁ пресича AC в точка M и AB – в точка N и хордата A₁B₁ пресича BC в точка R и AC – в точка S. Да се докаже, че:
    а) АA₁, BB₁ и CC₁ минават през една точка – O;
    б) АА₁ B₁C₁, BB₁ A₁C₁ и CC₁ A₁B₁;
    в) Ако O₁ е пресечната точка на AA₁ и B₁C₁, то О₁ е среда на AO;
    г) Правите MQ, NR и SP минават през точка O и MQ || AB, NR || AC и PS || BC.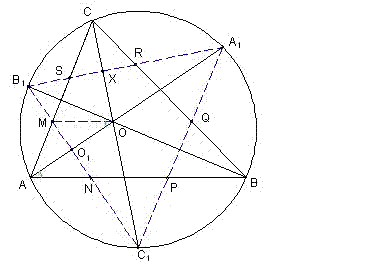

Доказателство:
Ще докажем, че АА₁, BB₁ и CC₁ са височини в A₁B₁C₁. Да означим с X пресечната точка на A₁B₁ с CC₁. Тогава B₁XC = (B₁C + C₁BA)/2 = (B₁C + C₁B + BA₁)/2 = (AC/2 + AB/2 + BC/2)/2 = 360^o/4 = 90^o, т.е. CC₁ B₁A₁.
Аналогично се доказва, че АА₁ B₁C₁ и BB₁ A₁C₁ . Това показва, че AA₁, BB₁ и CC₁ се пресичат в една точка, която означаваме с О. С това доказахме подусловията а) и б).
в) Да означим пресечната точка на АА₁ и B₁C₁с O₁. Доказахме, че О е ортоцентърът на триъгълника A₁B₁C₁. Съгласно доказаното в задача 11 точка A е симетрична на точка O относно B₁C₁, т.е. O₁ е среда на AO.
г) ANO₁ ≅ OM₁. Тогава O₁AN = O₁OM, т.е. MO || NA. Аналогично се доказва, че OQ || PB или MO || AB и OQ || AB , което показва, че точките M, O и Q лежат на една права и MQ || AB. Аналогично се доказва, че NR и SP минават през O и NR || AC и PS || BC.

Задача 10:
    Да се докаже, че окръжност, която разполовява трите страни на триъгълника, минава и през следните шест точки : петите на височините и средите на частите на височините, заключени между върховете и ортоцентъра (тази окръжност се нарича окръжност на Ойлер или окръжност на деветте точки).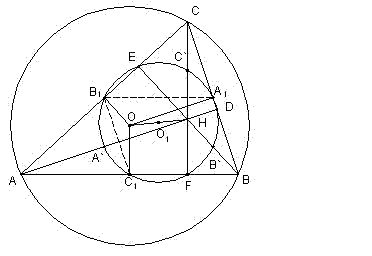

Доказателство:
    Нека точките A₁, B₁ и C₁ са средите на страните BC, CA и AB в триъгълника ABC, a H е ортоцентърът. Тъй като B₁ и A₁ са среди на страните AC и BC, то A₁B₁ е средна отсечка. Следователно A₁B₁ = AB/20 = C₁B (1) и A₁B₁ || AB (2). От (1) и (2) следва, че четириъгълникът B₁C₁BA₁ е успоредник и B₁C₁B = 180^o - C₁BA₁. От друга страна, B₁A₁F = B₁A₁B - FA₁B = 180^o - C₁BA₁ - (180^o + 2.C₁BA₁) = C₁BA₁. Следователно около четириъгълника B₁C₁FA₁ може да се опише окръжност, т.е. точка F лежи на окръжността с център O₁.Аналогично се доказва, че D и E лежат на тази окръжност. Да означим с A’, B’ и C’ средите съответнo на AH, BH и CH. A₁B₁A’ = AFC = 90^o като ъгли с взаимно успоредни рамене и A₁C₁A’ = AEB = 90^o. Следователно A₁B₁A’+ A₁C₁A’ = 180^o, с което показахме, че около A₁B₁A’C₁ може да се опише окръжност, т.е. точка А’ лежи на окръжността през точките А₁, B₁ и C₁. Аналогично се доказва, че точките B’ и C’ лежат на тази окръжност.

Задача 11:
    3а всеки остроъгълен триъгълник ABC да се намери такава точка P, че симетричните точки на P относно AB, BC и CA да лежат на описаната около триъгълника окръжност.

Доказателство:
    Ще докажем, че във всеки триъгълник ортоцентърът е такава точка. Нека H е ортоцентърът на ABC. Пресечните точки на правата AH със страната BC и описаната около ABC окръжност означаваме съответно с M и H₁. Тогава H₁CM = H₁B/2 = H₁AB = 90^o - ABM = HCM. От равенството на ъглите H₁CM и HCM следва еднаквостта на правоъгълните триъгълници H₁CM и HCM, които имат общ катет CM. Следователно точките H и H₁ са симетрични относно страната BC. С други думи точката, симетрична на ортоцентъра H относно страната BC, лежи върху описаната окръжност. Аналогично се доказва същото свойство и за другите две страни на ABC.