Геометрични построения - задачи по математика за 9 клас

Автор на статията е: Андон Илиянов Андонов, завършил НПМГ.

Първото построение, което ще разгледаме, е точен чертеж. Точният чертеж не е точно построение, но спада към групата, защото е нещо, което се прави, за да се улесни решението на задачата. Мнозина от читателите вероятно ще протестират, че точният чертеж не е и не може да бъде геометрично построение. В тяхна чест ще изложа една задача, която, колкото и невероятно да е, се решава с помощта на точен чертеж. Задачата е била давана на балканска олимпиада по математика, по идея на Гърция.

Условие: В окръжност к е вписан триъгълник ABC . Права пресича страните му AB и AC и продължението на BC съответно в точките D,F и E (C е между B и E). Хордите AM , BN и CP на к са успоредни на DE. Да се докаже, че ME,NF и PD минават през една точка.

Ако се вложат малко усилия в построяването на точен чертеж, веднага се забелязва, че точката на пресичане (обозначена на чертежа с “К”) лежи върху описаната около триъгълника окръжност. След това кратко, но ползотворно построение вече сме готови да преминем към съществената част от решението:
Нека ЕМ пресича к в точка К. EKC = MC/2 = MAC = EFC, така че EKFC е вписан в окръжност. Тогава FKC = FEC = CBN = CKN, така че K NF.
Аналогично K PD.

Както виждате, задачата е сравнително лесна и се решава на 4 реда, ако човек си направи труда за точен чертеж. Точният чертеж е препоръчителен при задачи с по-заплетени и сложни чертежи и особено при задачи с окръжности, защото тогава не може да се прецени на око.

Следващото построение, което ще бъде изложено, е пресичането на две от правите на чертежа. Това построение си няма точно име, но представлява пресичането на две или повече прави от чертежа с цел получаването на допълнителна точка, необходима за или улесняваща по -нататъшното решение на задачата. Неприятното при такива построения е фактът, че обикновено има твърде много възможности за построение и човек не знае кое ще му свърши работа. Затова пресичането на прави е препоръчително, когато знаем какво искаме да докажем и тръгваме отзад напред по стъпките на решението, намирайки точката, която ни трябва. Разбира се, може и просто да знаем как се решава задачата.

Прилагам задача, давана на областен кръг на национална олимпиада по математика през 2003 година.

Условие: Точка D се намира върху страната AC на ABC така, че BD = CD. През произволна точка E върху страната BC е построена права, успоредна на BD, която пресича AB в точка F. АЕ пресича BD в точка G. Да се докаже, че BCG = BCF.

Решение:
Продължаваме правата FE до пресичането и с AC в точка H.
CDG = FHC, понеже DB || FH;
CD/DG = BD/DG = FH/HE = FH/HC;
Тогава CDG е подобен на FHC
=> GCD = CFH, откъдето
BCG = BCD - GCD = CEH - CFH = BCF.

Това са първите две най-базисни построения в геометрията, които обаче съвсем не са достатъчни, защото в повечето задачи те са нещо обикновено, съпътстващи другите построения. Но преди да преминем нататък, ще изложим една задача, която обобщава и допълва тези две базисни построения, вмъквайки едно ново построение – медиана или построяване среда на отсечка.

Условие: Даден е вписан петоъгълник ABCDE, в който AC || DE и точка M е средата на BD. Да се докаже, че ако AMB = BMC, то BE разполовява AC.

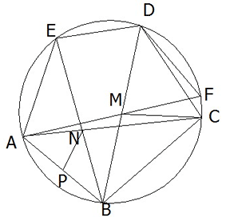
Нека BE ∩ AC = N и P е средата на AB.
Означаваме
BAC = BDC = α
ABE = CBD = β
ADB = ACB = γ.

Тогава ABN ≈ DBC и тъй като NP и CM са съответни медиани в тези триъгълници, имаме
BPN ≈ BMC.

Нека AMB = BMc = φ
=> BPN = φ

Ще използваме следния факт: Ако две хорди разполовяват трета и сключват с нея равни ъгли, то те са равни помежду си и се разделят на съответно равни части от пресечната си точка. Нека AM пресича k в точка F. Тогава CM = FM
=> BMC ≅ DMF
=> BC = DF
MAD = BDC = α
От AMD получаваме
φ = α + γ
От тук и от APN заключаваме, че
ANP = φ - α = γ = ACB.
Тогава NP || BC, т.е. NP е средна отсечка в ABC и N е среда на AC, с което условието е доказано.

С тази задача приключихме началния пакет от базисни построения, които са необходими за решаването на голяма част от задачите. До такава степен сме свикнали с тях, че дори не ги броим за геометрични построения, но истината е, че те значително улесняват решаването на задачите. Сега ще преминем към някои от по-съществените построения.

Построяване на окръжност.

Условие: Върху страните BC и CD на квадрата ABCD са избрани точки M и N така, че MAN = 45°. Да се докаже, че центърът на описаната окръжност около триъгълника AMN лежи на диагонала AC на квадрата ABCD.

Описваме окръжност около триъгълника CMN и пресечната и точка с диагонала AC означаваме с O. Ще докажем, че точка О е центърът на описаната около AMN окръжност.
MON = 90° = MCN
OM = ON, CA е ъглополовяща в CMN и на равни дъги отговарят равни хорди: OM = ON, OM = ON.
=> точка О е центърът на описаната около AMN окръжност.

Спускане на перпендикуляр към дадена права.

Още едно от базисните построения, без които просто не можем. Задачата, която съм приложил, е съставена по моя идея, но не претендирам за авторски права. Въпреки че трудността и не е голяма, съм я избрал заради подхода към решението (изразяване чрез лица), който е тясно свързан с разглежданото геометрично построение.

Условие:
Даден е равностранен триъгълник ABC и произволна точка от вътрешността му O. От точка O са построени отсечки OP,OQ и OM, свързващи я съответно със средите на страните на триъгълника. Да се докаже, че OP + OQ + OM ≥ h, където h е височина в триъгълника.

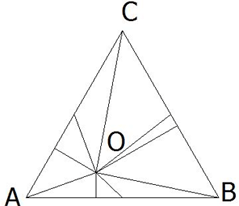
Р-е: Спускаме перпендикулярите от точка O към страните на триъгълника. Нека ги обозначим съответно p_a, p_b и p_c. След това построение задачата ни вече е почти решена.
S_ABO = AB.p_c/2,
S_BOC = BC.p_a/2,
S_AOC = AC.p_b/2;
=> S_AOb + S_AOC + S_BOc = (AB.p_c + BC.p_a + AC.p_b)/2
Но AB = BC = AC по условие.
=> S_AOB + S_BOC + S_AOC = AB(p_c + p_b + p_a)/2
Но S_AOB + S_AOC + S_BOC = S_ABC = AB.h_a/2
=> p_a + p_b + p_c = h.
Bсеки от получените малки триъгълници е правоъгълен с хипотенузи съответно OP,OQ и OM и бедра p_a, p_b и p_c.
=> OP > p_c;
OQ > p_a;
OM > p_b;
От това директно следва, че OP + OQ + OM > h. Равенството се получава, когато О е център на триъгълника и OP,OQ и OM съвпадат с p_a, p_b и p_c.

Построяване на успоредна права.

Ще съчетаем това построение с някои от вече споменатите построения, тъй като задачите, към които сме се насочили, повишават трудността си. Както е казал Шаригин – “Първи възвишения”. Всъщност построяването на успоредна права е изключително разпространено построение, което се използва в много задачи включително и всеизвестните помощни задачи.

Условие:
Диагоналите на трапец имат дължини съответно 3см и 5см, а отсечката, съединяваща средите на двете му основи, има дължина 2 см. Да се намери лицето на трапеца.

Решение:
Hека точка K AB и
CK || DB
S_tr = (AB + CD)h/2      (1)
S_AKC = (AB + BK)h/2      (2)
(1) + (2) => S_AKC = S_ABCD
Построяваме CL || PN (където PN свързва средите на двете основи).
=> |CL| = |PN| = 2 Продължаваме CL така, че LM = CL.
|AL| = a/2 + b/s
=> точка L е средата на AK.
S_CMK = S_AKC = S_ABCD

Обаче ние знаем страните на ACK и поради техните широкоизвестни стойности знаем, че той е правоъгълен. От там лесно можем да намерим лицето му.

Важно е да се посочи, че ние можем да намерим лицето му дори и без да използваме факта, че е правоъгълен, ако използваме Хиронова формула. Това би представлявало един по-интересен вариант на задачата, където имаме дадени два диагонала и отсечка, свързваща средите на страните.

В такъв случай отговорът би бил √p(p - 2c)(p - a)(p - b), където a и b са двата диагонала, c е отсечката, а p = (a + b + 2c)/2.

Ето още една задача, която включва в решението си построяването на успоредна права, както и няколко други също така интересни построения. Надявам се задачата да представлява интерес за читателя, въпреки че не се отличава с някаква особена трудност, като изключим досещането за построенията.

Условие:
Върху бедрата KL и MN на равнобедрения трапец KLMN са избрани съответно точките P и Q такива, че отсечката PQ е успоредна на основите. Знае се, че във всеки от трапеците KPQN и PLMQ може да се впише окръжност с радиуси съответно R и r. Да се намерят основите |LM| и |KN|.

Решение:
Първо, от центровете на двете окръжности спускаме перпендикуляри към бедрото KL. От центъра на малката окръжност построяваме права, успоредна на KL. Получаваме правоъгълен триъгълник с хипотенуза R + r, катет R - r и остър ъгъл α, равен на острия ъгъл на трапеца. Получаваме, че:
cos α = (R - r)/(R + r)
Голямата основа е равна на
2Rcotg(α/2) = 2R
а малката основа е равна на
2rtg(α/2) = 2r.

И така, след като сме минали през построяването на успоредна права, вече е време за някои по-сериозни построения. Без повече обяснения смело пристъпваме към следващото геометрично построение – построяване на триъгълник. То е едно доста полезно и предизвикателно построение, с което шега не бива. В негова чест ще изложа тази задача.

Условие:
В квадрат ABCD е взета точка M така, че MAB = 60°, MVD = 15°. Да се намери MBC.

Решение:
На страната AB вътре в квадрата ABCD построяваме равностранен триъгълник ABK.
Понеже KAB = MAB = 60°, то точка М лежи на правата AK.
Но DCK = 15° = MCD, от където следва, че М лежи на правата KC. Получаваме M ≡ K => MCB = 30°.

След като заговорихме за построяване на триъгълници, няма как да изпуснем и една от главните фигури в геометрията. Всъщност това е една от главните фигури не само в геометрията, защото въплъщава в себе си представата за идеал и съвършенство. И така напред към следващото построение – построяване на окръжност. С цел компактност няма да създавам отделни точки за вътрешновписаните и външновписаните окръжности, както и за всички останали.

Условие:
За триъгълник ABC е построена права, пресичаща страните AC и BC съответно в точки M и N така, че MN = AM + BN. Да се докаже, че всички такива прави се допират до една и съща окръжност.

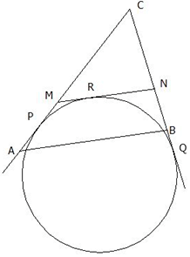
Решение:
Построяваме външновписаната окръжност за MCN.
Имаме MP = MR, NQ = NR,
=> MN = MP + NQ
Но по условие MN = MA + NB.
По такъв начин една от точките P и Q лежи върху страна, а другата – на продължение. При това
CP = (CP + CQ)/2 = (AC + CB)/2
т.е. построената окръжност е постоянна за всички прави MN.

След като преминахме запознаването с различните геометрични построения, е време да преминем към главните задачи. Те няма да са много, но затова пък ще са трудни и класически задачи, които не могат да бъдат решени без помощта на геометрични построения. Надявам се да видите красотата в тези задачи, въпреки необичайното им естество.

Долуизложената задача е в раздел “Геометрични неравенства и екстремални задачи в планиметрията”. Моля не опитвайте това сами във вкъщи!!!

Условие:
В ABC са построени медианитие BM и CN. Да се докаже, че ако MB е перпендикулярна на CN, то cotgβ + cotgγ ≥ 2/3 (използвани са стандартни означения).

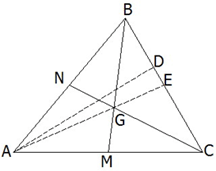
Нека AD е височина, а AE е медиана в ABC.
BM ∩ CN ∩ AE = G
тогава cotgβ + cotgγ =
= |BD|/|AD| + |CD|/|AD| = |CB|/|AD| ≥ |CB|/3|GE|
Но |CB|/|GE| = 2
Получаваме cotgβ + cotgγ ≥ (1/3).2

Следващата задача също е с повишена трудност, така че моля: ако правите експерименти; взимайте мерки за безопасност! Препоръчителен учителски контрол: 9 клас.

Условие: Върху страните на даден ABC външно за триъгълника са построени квадратите BCEF, CAGH и ABKL. Да се докаже, че симетралите на отсечките EH, GL и KF се пресичат в една точка.

Решение:
Нека s_a, s_b и s_c са симетралите сътветно на отсечките GL, KF и EH. Построяваме и симетралите на AG, BK и CE. Те образуват триъгълник A₁B₁C₁. Точка A₁ е обща за симетралите на страните AG и AL на триъгълника AGL. Следователно през нея минава и симетралата s_a на отсечката GL.

По аналогичен начин доказваме, че s_b минава през B₁, а s_c - през C₁; Важна част от решението на задачата е хомотетичността на триъгълника ABC и допълнително построеният триъгълник A₁B₁C₁ . Наличието на тази хомотетия следва веднага от успоредността на AB и A₁B₁, на BC и B₁C₁, както и на CA и C₁A₁. С оглед на тази хомотетия е достатъчно да докажем, че s_a, s_b и s_c са успоредни на медианите на триъгълника ABC, защото в такъв случай ще получим, че и s_a, s_b и s_c са медиани в триъгълника A₁B₁C₁, а това означава, че имат обща точка (медицентър).

Нека CD е медиана на триъгълника ABC. Ще докажем, че s_c || CD, т.е. CD e перпендикулярна на EH:
CD.EH = (CA + CB)(CH - CE)/2
= (-CACE + CB.CH)/2
(използваме, че CA е перпендикулярна на CH & CB е перпендикулярна на CE);
Триъгълниците AEC и HBC са еднакви
=> CACE = CBH
Като обединим получените по-горе равенства, получаваме следното:
CD.EH = 0; или CD е перпендикулярна на EH;
С това твърдението е доказано.