Задачи за вектори
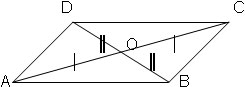
1. Да се докаже, че всеки четериъгълник, чийто диагонали се разполовяват от пресечната им точка, е успоредник.
Решение:
По условие имаме 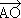 =
=  и
и 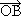 =
= 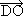
Като съберем почленно равенствата, получаваме
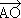 +
+ 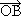 =
= 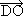 +
+  т.е.
т.е.  =
= 
Следователно четериъгълникът АВСD е успоредник.
2. Дадени са векторите  и
и  . Да се построи вектор, равен на:
. Да се построи вектор, равен на:
3 + 2
+ 2
3 - 2
- 2
Решение:
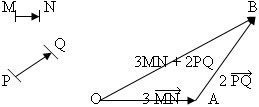
От произволна точка О построяваме  = 3
= 3 , а от точка А построяваме вектор
, а от точка А построяваме вектор  = 2
= 2 ; векторът
; векторът 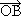 е търсеният,т.е.
е търсеният,т.е.  = 3
= 3 + 2
+ 2 
От точка О построяваме вектор  = 3
= 3 , а от точка А построяваме вектор
, а от точка А построяваме вектор
 = -2
= -2  ; векторът
; векторът  е търсеният, т.е.
е търсеният, т.е. 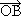 = 3
= 3 - 2
- 2 
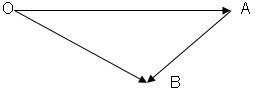
3. Дадени са векторите  и
и  . Да се провери геометрически верността на тъждеството(
. Да се провери геометрически верността на тъждеството( +
+  ) +(
) +( -
-  ) = 2
) = 2
Решение:

Построяваме с начало произволна точка О вектор  =
=  и с начало точка А – вектор
и с начало точка А – вектор  =
=  Векторът
Векторът 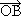 =
=  +
+  След това построяваме с начало В – вектора
След това построяваме с начало В – вектора  =
=  и с начало С – вектора
и с начало С – вектора  = -
= -  .
.
Векторът 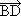 =
=  -
-  . От успоредника АDCB имаме
. От успоредника АDCB имаме 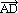 =
=  =
=  Следователно,
Следователно, 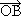 +
+ 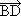 =
=  =
=  +
+ 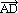 = 2
= 2 ,
,
т.е.(  +
+ ) + (
) + ( -
-  ) = 2
) = 2
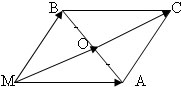
4. Точката О е среда на отсечката АВ, а М – произволна точка. Да се докаже, че 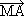 +
+ 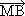 = 2
= 2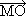
Решение:
Построяваме успоредника МАСВ, в който 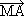 +
+ 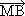 =
= 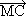 . Но тъй като диагоналите в успоредника се разполовяват, имаме
. Но тъй като диагоналите в успоредника се разполовяват, имаме 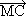 = 2
= 2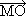 , откъдето
, откъдето 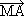 +
+ 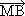 = 2
= 2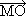
5.Да се докаже, че е възможно да построим триъгълник, на който страните са равни и успоредни на медианите на даден триъгълник АВС
Решение:
Да означим с А1, В1,С1 средите на страните ВС, АС, и АВ, а с 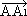 ,
, 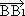 ,
, 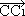 - векторите, които съвпадат съответно с медианите АА1,ВВ1,СС1; тогава
- векторите, които съвпадат съответно с медианите АА1,ВВ1,СС1; тогава
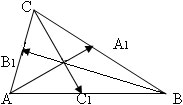
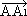 =
=  +
+  / 2;
/ 2; 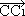 =
= 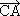 +
+ /2;
/2; 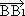 =
=  +
+ 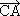 / 2
/ 2
като съберем почленно тези равенства, получаваме:
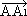 +
+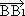 +
+ 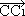 =
=  +
+  /2 +
/2 +  +
+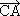 / 2 +
/ 2 + 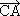 +
+  /2 =
/2 =
3/2( +
+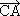 +
+ ) = 0
) = 0
т.е.
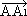 +
+ 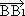 +
+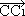 = 0,
= 0,
следователно векторите 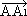 ,
, 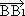 , и
, и 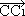 образуват триъгълник
образуват триъгълник
Задачи за упражнения:
1. Върху векторите  и
и 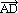 е построен успоредникътАВСD. Намерете диагоналите на успоредника
е построен успоредникътАВСD. Намерете диагоналите на успоредника
Отг.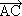 =
=  +
+ 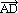 ,
, 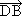 =
=  -
- 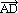
2. Проверете геометрически верността на тъждествата:
( +
+  ) – (
) – ( -
-  );
);
 + (
+ ( -
-  ) =
) =  ;
;
( -
- )/2 +
)/2 + = (
= ( +
+  )/2
)/2
3. В успоредника АВСD О е пресечна точка на диагоналите, а М е произволна точка от равнината на успоредника. Докажете равенството:
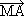 +
+ 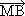 +
+ 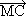 +
+ 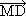 = 4
= 4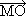
4. Докажете, че ако M е център на тежестта на триъгълника АВС, то
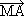 +
+ 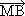 +
+ 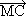 = 0
= 0
5. Докажете, че ако съединим последователно средите на страните на произволен четириъгълник получаваме успоредник.
6. Върху оста Х са дадени точките А(а) и В(b). Намерете абсцисите на средата на отсечката АВ и на точките, които разделят АВ на три равни части. Решете задачата при а = +15, b = -9
Отг. +3; -1; +7
Вектори - определения
Равенство на вектори
Произведение на вектор с число
Сбор и разлика на вектори
Задачи за вектори

 Меню
Меню