Стереометрия - определения
Отношение между права и равнина
Права а лежи в равнина α, ако: • има две общи точки с равнината
• има две общи точки с равнината
• има обща точка с α и е успоредна на права от α
• има обща точка с α и е успоредна на права b, която е успоредна на α
• има обща точка с α и е перпендикулярна на права b, която е перпендикулярна на α
• има обща точка с α и е перпендикулярна на равнина β, която е перпендикулярна на α
Права а е успоредна на равнина α, ако:
• няма обща точка с α
• е успоредна на права от α
• е перпендикулярна на права, която е перпендикулярна на α
• е перпендикулярна на равнина, която е перпендикулярна на α
Права а е перпендикулярна на равнина α, ако: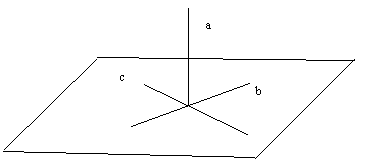
• е перпендикулярна на две пресичащи се прави от α
• е успоредна на права, която е перпендикулярна на α
• е перпендикулярна на равнина, която е успоредна на α
• лежи в равнина, перпендикулярна на ? и е перпендикулярна на пресечницата на две равнини
Ако правата а е перпендикулярна на равнина α, то всяка права от равнината е перпендикулярна на а.
Разстояние между успоредна права и равнина е разстоянието d от коя да е точка от правата до равнината.
Ъгълът между права и равнина е ъгълът между правата и нейната ортогонална проекция върху равнината.
Две прави в пространството могат да бъдат – кръстосани, перпендикулярни или успоредни.
Взаимно отношение на две прави в пространството
Две прави са кръстосани, ако:
• не съществува равнина, която ги съдържа.
• Ъгъл между две кръстосани прави е ъгълът между две пресичащи се прави успоредни на кръстосаните.
Две прави са перпендикулярни, ако:
• ъгълът между тях е 90°;
• едната права е перпемдикулярна на равнината в която лежи другата права.
Две прави в пространството са успоредни, ако:
• една от тях е успоредна на пресечницата на двете равнини, които ги съдържат;
• са пресечници на две успоредни равнини с трета.
Взаимно положение на две равнини
Две равнини съвпадат, ако имат три общи различни точки.
Две равнини са успоредни, ако:
* нямат обща точка.
* две пресичащи се прави от едната равнина са съответно успоредни на две пресичащи се прави от другата.
* всяка от тях е успоредна на трета равнина.
През всяка точка, нележаща в дадена равнина съществува единствена равнина, успоредна на дадената.
Всяка права, лежаща в една от две успоредни равнини е успоредна на втората.
Две равнини са перпендикулярни, точно когато двустенният ъгъл между тях е прав.
Призма
Определение: Многостен, две от стените на които са еднакви n -ъгълници, разположени в успоредни равнини, а другите му стени са успоредници, се нарича n -ъгълна призма.
Права призма - призма на която околните ръбове са перпендикулярни на основите.
Правилна призма – права призма основата на която е правилен n -ъгълник.
Височина на призма – всяка отсечка крайщата на която лежат в двете основи на призмата и е перпендикулярна на тях. Това е разстоянието между равнините на двете основи.
Околната повърхнина на призма е сумата от лицата на околните стени.
Пълна повърхнина - сумата от околната повърхнина и лицата на основите се нарича ( или лице на повърхнина на призма).
Лицето на околната повърхнина S = l . p , където l – дължината на околният ръб, а р периметъра на перпендикулярното сечение( за права призма периметъра на основата).
Лицето на пълната повърхнина S1 = S + 2. B , където В е лицето на основите. Обемът V = B . H , където H – височината на призмата.
Пирамида
Oпределение: Многостен една от стените на който е многоъгълник, а останалите стени са триъгълници с общ връх, нележащ в равнината на многоъгълника се нарича пирамида.
Височина на пирамидата е отсечката, единият край на която е върха на пирамидата, а другият е проекцията му върху равнината на основаtа.
Височината на което и да е околна стена от върха на пирамидата към основният ръб се нарича апотема.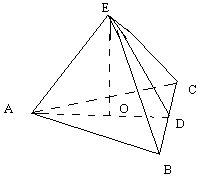
Правилна пирамида - пирамида, с основа правилен многоъгълник и равни околни ръбове.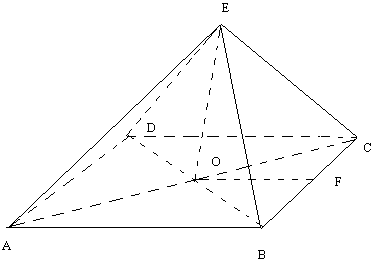
Лицето на околната повърхнина на правилна n-ъгълна пирамида е:
S = n(a.k)/2 = P.k/2,
където k е апотемата, аР е периметъра на основата.
Лицето на пълната повърхнина е
S1 = S + B.
Обемът на пирамида е V = BH/3, където В е лицето на основата, а Н е височината на пирамидата.
Пресечена пирамида
Частта от пирамида заключена между две нейни успоредни сечения се нарича пресечена пирамида.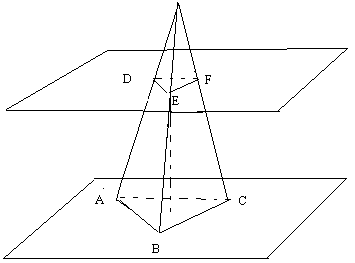
Правилната пресечена пирамида има:
• Равни ръбове на долната основа;
• Равни ръбове на горната основа;
• Равни околни ръбове;
• Всички околни стени са равнобедрени трапеци.
И тук както при обикновената пирамида височината в околната стена се нарича апотема.
Цилиндър
Фигура заключена между два еднакви кръга се нарича цилиндър.
Отсечката свързваща съответни точки от двете основи се нарича образувателна.
Ако образувателната на цилиндъра е перпендикулярна на основите, то цилиндъра е прав кръгов.
Отсечката свързваща центровете на двете окръжност се нарича ос на цилиндъра.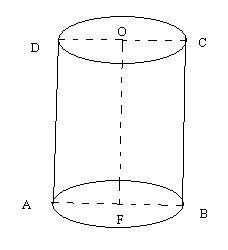
Цилиндъра може да се разгледа и като ротационно тяло получено при въртенето на правоъгълник около една негова страна.
Около всеки прав кръгов цилиндър може да се опише сфера, като центъра u е средата на оста.
В = π r2 - лице на основата.
S = 2 π . r . l – лице на околна повърхнина на прав кръгов цилиндър.
S1 = S + 2. B = 2. π . r .( r + l ) – лице на пълна повърхнина на прав кръгов цилиндър.
V = π . r 2 . h – обем на кръгов цилиндър.
Конус
Множество от точки лежащи между кръг и точка нележаща в равнината на този кръг се нарича конус.
Фигура получена при въртенето на правоъгълен триъгълник около негова страна се нарича конус.
Точката нележаща в равнината на кръга се нарича връх.
Кръга наричаме основа на конуса.
Отсечката минаваща през центъра на основата и върха на конуса се нарича ос на конуса.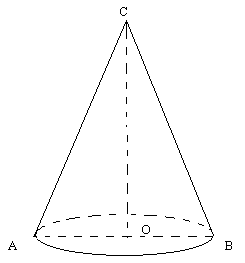
Разстоянието от върха на конуса до равнината на основата е височина на конуса, ако той е прав то височината съвпада с оста.
Отсечката свързваща върха на конуса с точка от кръга се нарича образувателна.
S = π . r . l - лице на околна повърхнина на прав кръгов конус.
S1 = S + B – лице на пълна повърхнина на прав кръгов конус, където В е лицето на основата.
V = BH/3 = (1/3)πr2.H - обем на прав кръгов конус.
Пресечен конус
Тяло, което е част от кръгов конус, заключена между две успоредни сечения се нарича пресечен конус.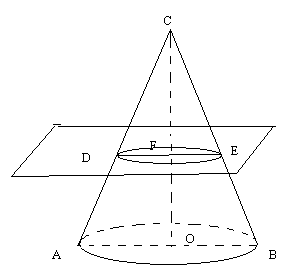
Разстоянието между равнините се нарича височина на пресечения конус.
Отсечката свързваща основите на пресечения конус се нарича ос.
Ако оста на пресечения конус е перпендикулярна на равнините на основите, то пресечения конус е прав.
S = π(r + r1). – лице на околна повърхнина на прав кръгов пресечен конус.
S1 =S + B + B1 – лице на пълна повърхнина на прав кръгов пресечен конус.
V = π.h.(r2 + r21 + r.r1)/3 – обем на прав кръгов пресечен конус.
Кълбо и сфера
Сферата е множество от точки в пространството, които се намират на дадено разстояние R от дадена точка О – център на сферата.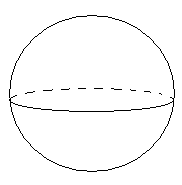
Хорда на сфера – отсечка коята свързва две точки от сферата.
Диаметър на сферата – хорда която минава през центъра на сферата.
Сечението на равнина със сфера винаги е окръжност, а ако тази окръжност минава през центъра на сферата, то тя се нарича голяма окръжност.
Сферата може да се получи и като ротационно тяло при въртенето на полуокръжност около диаметъра си.
Лицето на повърхнината на сфера е S = 4.π. R2
Лицето на сферичен отрез е S сферичен отрез = 2.π. R.h, където h = PQ.
Кълбото е множество от точките на сферата и всички нейни вътрешни точки.
Обемът на кълбо е V = (4/3) .π. R3
Обемът на отрез от кълбо е V отрез от кълбо = (1/3) .π. h2(3. R – h).

 Меню
Меню