МенюПроизведение на вектор с число
Ако k е число, а 
вектор, то произведение k.AB (или AB.k) се нарича всеки вектор 
, който лежи върху директрисата на или върху успоредна на нея права, има дължина, равна на |k|.||, и посока, съвпадаща с тази на или противоположна на нея, според това, дали k > 0 или k < 0
Тогава пишем
= k.
Ако k = 0 или е нулев вектор(или ако са изпълнени и двете условия) произведение k. е всеки нулев вектор.
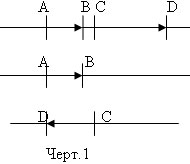
Така от черт.1 се вижда, че = +1,5., a = -1,5
Отношение на два вектора
Ако и са два вектора върху една и съща права или успоредни прави и при това не е нулев вектор и || и || са дължините на тези вектори, то частното ± || : || се нарича отношение на векторите и . Отношение на два вектора е релативно число(положително, отрицателно или нула), абсолютната стойност на което е равна на частното от дължините на двата вектора, а знакът му е + или – според това, дали векторите са еднопосочни, или разнопосочни.
Обратно, ако и са вектори върху сливащи се или успоредни прави и не е нулев вектор, то векторът е произведение на с някакво число k( = k.), където k = :
Нека върху оста Х са дадени сегментите и (черт.2) Тогава
: = - 3/5 или = -3/5
и
: 
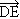= +3/2 или = +3/2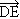
Право противоположни вектори имат равни дължини и противоположни посоки.
Така от чертежа се вижда, че
/ 
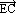= +1 или = 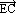и
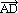/ = -1 или = -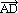
В частност /
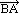= -1 или = - 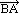и АВ = -ВА
означва че има стрелка отгоре т.е. е (вектор)
Следователно:
И така, равенствата: / = k, / = 1/k, = k. и = 1/k. където k е релативно число, показват, че:
Правите AB и CD са успоредни или се сливат;
Отношението на отсечките AB и CD е равно на |k|;
Векторите и са еднопосочни или разнопосочни според това, дали |k| е положително, или отрицателно число.
Вектори - определения
Равенство на вектори
Произведение на вектор с число
Сбор и разлика на вектори
Задачи за вектори
