Kooрдинатни системи и графики на функции

Правоъгълна координатна система се състои от две перпендикулярни прави, наречени координатни оси, които се поставят така, че се пресичат в началата си.

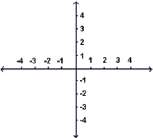
Кръщаването на осите с х и у е най-често срещано, но може да се нарекат с каквито и да е други букви. Ако са използвани буквите х и у, то равнината се нарича ху-равнина. В приложенията често се използват други букви освен х и у,както е показано на долните фигури, като uv-равнина или ts-равнина.

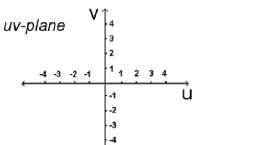
Наредена двойка

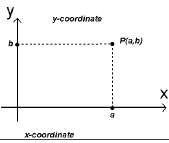
Под наредена двойка ще разбираме две реални числа в определен ред. Всяка точка Р в координатната равнина може да бъде свързана с единствена наредена двойка реални числа като прекараме две прави през точката Р, едната перпендикулярна на оста х,а другата - на оста у.

Правоъгълната координатна система се състои от две перпендикулярни координатни прави, наречени координатни оси, които са разположени така, че се пресичат в началата си.

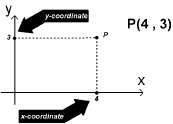
Например, ако вземем (a,b)=(4,3), то на координатната равнина това ще изглежда по следния начин:

Кръщаването на осите с буквите х и у е често срещано, но могат да бъдат използвани които и да е букви. Ако осите са кръстени с буквите х и у, то получената равнина ще се нарича ху-равнина. В приложенията често се използват и други букви освен х и у, както е показано на следващите фигури, като например uv-равнина и ts-равнина.

Да се начертае точка Р(a,b) значи да се разположи точката със координати (a,b) в координатната равнина. Например, на фигурата са нарисувани различни точки.

В правоъгълна координатна система координатните оси разделят равнината на четири области, наречени квадранти. Те се номерират по посока обратна на часовниковата стрелка с римски цифри, както е показано

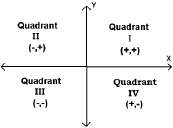
Дефиниция за графика

Графиката на уравнение с две неизвестни х и у е множеството от точки в равината, чийто координати са решения на това уравнение.

Пример: Начертайте графиката на
Графиката на у=х²

Tова е приближение на графиката на у=х².По принцип, само с техники от алгебрата може да определи истинската форма на графиката.

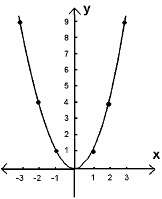
Пример: Начертайте графиката на у = 1/х.

Понеже 1/х не е дефинирано, когато х = 0, можем да чертаем точки, за които х ≠ 0.

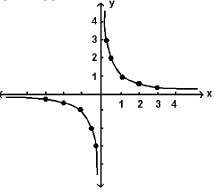
Пример: Намерете всички пресечни точки на
(а) 3х + 2у = 6f
(b) x = y² - 2yf
(c) y = 1/x

Решение:

3x + 2y = 6 пресича х.
Тогава приравняваме у на 0 и решаваме за х 3х = 6 или х = 2
e търсената пресечница с х.
Аналогично и замествайки с х = 0 намираме, че търсената пресечна точка с у е у = 3.

По същия начин се решава (b), а (c) е решено тук

y = 1/x

x - пресечница

Приравняваме у на 0 1/х = 0 → x не е дефинирано, т.е. няма никакви пресечни точки, нито х, нито у.

Приравнявайки х на 0

у = 1/0 → y не е дефинирано → няма пресечни точки по у.

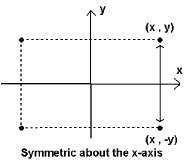
На долната фигура, точките (х,у),(-х,у),(х,-у) и (-х,-у) определят върховете на правоългълник.

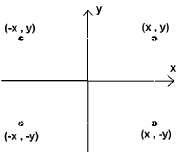
• симетрична спрямо оста х, ako за всяка точка (х,у) на графиката, точката (х,-у) също е на графиката.

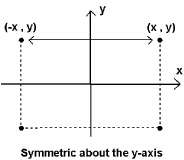
• симетрична спрямо оста y, ako за всяка точка (х,у) на графиката, точката (-х,у) също е на графиката.

• симетрична спрямо центъра, ако за всяка точка (х,у) на графиката, точката (-х,-у) също е на графиката.

Дефиниция:

Графиката в равнината на функцията f е дефинирана да бъде графиката на уравнението у = f(x)

Пример: 1
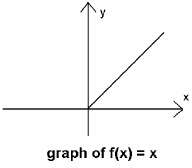
Начертайте графиката на f(x) = x + 2

y = x + 2

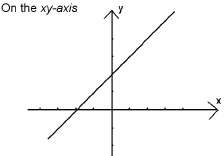
графика на f(x) = x + 2.

Пример: 2 Начертайте графиката на f(x) = |x|

y = |x|

|x| =

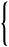
x, ако x ≥ 0, т.е. x is неотрицателно -x, ако x < 0, т.е. x отрицателно

Графиката съвпада с правата у = х за х ≥ 0 и с правата у = -х за х < 0.
     

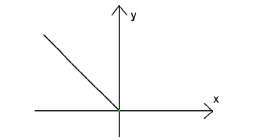
графика на f(x) = -x
Koмбинирайки тези две графики, получаваме

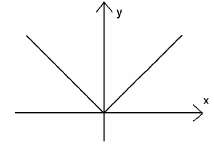
графика на f(x) = |x|.

Пример: 3 Начертайте графиката на функцията

t(x) = (x² - 4)/(x - 2) =

= ((x - 2)(x + 2)/(x - 2)) =

= (x + 2)     x ≠ 2.

Оттук тази функция може да бъде записана като

y = x + 2     x ≠ 2

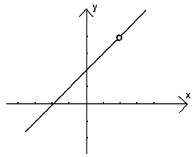
Графиката на h(x) = x² - 4.

Пример: 4 Начетайте графиката на

g(x) =

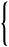
1      if x ≤ 2 x + 2      if x > 2

Чертаене на графики на функции чрез транслация

- Представете си, че знаем графиката на f(x)

- Тогава можем да открием и графиките на

y = f(x) + c

y = f(x) - c

y = f(x + c)

y = f(x - c)

y = f(x) + c       графиката на f(x) се транслира НАГОРЕ с с единици

y = f(x) - c       графиката на f(x) се транслира НАДОЛУ с с единици

y = f(x + c)       графиката на f(x) се транслира НАЛЯВО с с единици

y = f(x - c)       графиката на f(x) се транслира НАДЯСНО с с единици

Пример: 5 Начертайте

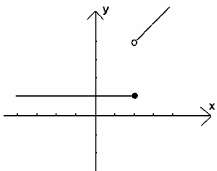
графиката на у = f(x) = |x - 3| + 2

Tранслирайте графиката на у = |x| 3 единици НАДЯСНО, за да получите графиката на

y = |x - 3|

Сега транслирайте графиката на y = |x - 3| 2 единици НАГОРЕ, за да получите графиката на у = |x - 3| + 2

Пример: 6

Начертайте графиката на

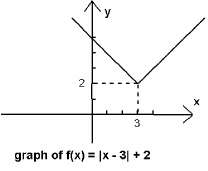
y = x² - 4x + 5

допълнете до точен квадрат

y + 4 = (x² - 4x + 5) + 4        y = (x² - 4x + 4) + 5 - 4

y = (x - 2)² + 1

В тази форма виждаме, че графиката може да бъде получена чрез транслиране на графиката y = x² надясно с 2 единици заради x - 2, и нагоре с една единица заради and up + 1.

Отражения

(-x, y) е отражеие на (x, y) спрямо оста y

(x, -y) e отражение на (x, y) спрямо оста x

Графиките на y = f(x) и y = f(-x) са отражения една на друга спрямо иста у

Графиките на y = f(x) и y = -f(x) са отражения една на друга срямо оста х

Графиката може да бъде постигната чрез отражение и транслация:

- Начертайте графиката на

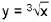
- Отразете я спрямо оста у за да получите графиката на

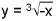
-  Транслирайте тази графика надясно с 2 единици за да получите графиката на

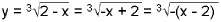
Toва е графиката на



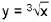
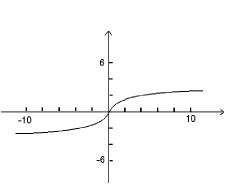
Ako f(x) се умножи с положителна константа с

Графиката на f(x) се стеснява вертикално, ако 0 < c < 1

Графиката на f(x) се разширява вертикално, ако c > 1

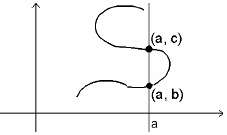
Кривата не е графика на у = f(x) за която и да е функция f.