Условия, които свързват корените на квадратно уравнение с числа и интервали от числа

За кои стойности на параметъра "k" квадратното уравнение:
            2x² + (2k-1)x + k - 1 = 0
има точно един корен между числата -1 и 0, а другият е по голям от ½.
За да достигнем до твърдението, което ще помогне при решаването на задачата, ще се спрем на следните помощни задачи:

1. Как най-бързо, но не и точно, може да построи графиката y = x² - 4?
За да се отговори на поставения въпрос е необходимо да се намерят точките, в които графиката пресича координатните оси (тук не се иска точно прострояване на графиката).
Точката, в която графиката пресича ординатната ос, се получава при х = 0, т.е. (0,-4). При у = 0 получаваме (х - 2)(х + 2) = 0 или (-2,0) и (2,0). Графиката най-грубо изглежда така, както е показана на фигурата.

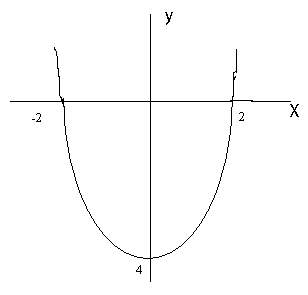
Как ще изглежда графиката на функцията у = -4x² + 1?
Аналогично на предната задача се получават точките: (0,1); (-½,0); (½,0), а графиката ще има вида

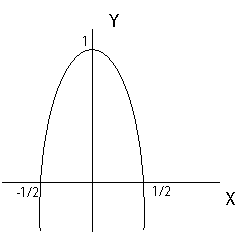
Тези два чертежа помагат да се разберат понятията вдлъбната и изпъкнала парабола в зависимост от коефициента пред втората степен на х. Тези термини не е необходимо да се използват, достатъчно е само - парабола с връх нагоре или надолу.

3. За кои стойности на параметъра "а" уравнението x² - 4x + a - 1 = 0 притежава реални и различни корени, така че числото 2 да е между корените му.
За решаването на тази задача е необходимо да се премине през няколко етапа:
a) За да притежава уравнението реални и различни корени трябва D₁* = 2² - (a - 1) = 5 - a > 0, т.е. a < 5
б) Как ще изглежда графиката на функцията y = x² - 4x + a - 1 спрямо абцисната ос?

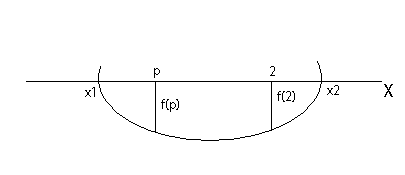
Понеже коефициентът пред x² е положително число и при стойности на параметъра по-малки от 5 квадратния тричлен има два реални и различни корена, то графиката на функцията ще бъде парабола с връх надолу, която пресича в две различни точки абцисната ос x₂ и x₁.
Да разгледаме каква ще бъде стойността на функцията за точката p от оста. Алгебричната мярка на отсечката, с която се размерва стоийността на функцията, е отрицателно число. Това се отнася за всички точки от интервала (x₂, x₁). Условието числото 2 да е между корените на уравнението означава: f(2) < 0.
в) Решаванве на системата:
           |f(2) < 0
           |a < 5.

4. За кои стойности на отрицателното число "k" уравнението kx² + 11x - 5 = 0 има релани и различни корени такива, че числото 1 да е между тях.
Аналогично на задача 3 за решаване на тази задача се преминава през същите етапи, за да се стигне до извода, че условието числото 1 да принадлежи на интервала (x₂,x₁) e равнозначно на f(1) > 0.

От двете помощни задачи се стигна до обощението: за да принадлежи дадено число "р" на интервала от корените на квадратонто уравнение, то трябва a.f(p) < 0, което може да се изкаже така:

НЕОБХОДИМОТО И ДОСТАТЪЧНО УСЛОВИЕ "р" да принадлежи на интервала (x₂,x₁) на квадратното уравнение ax² + bx + c = 0 e a.f(p) < 0
Необходимост:
Нека x₂ ≠ x₁ и р (x₂,x₁).
Ще докажем, че а.f(p) < 0.
Доказателство:
Щом x₁ ≠ x₂ съществуват и са релани числа, то:
ax² + bx + c = 0 = a(x - x₁)(x - x₂), тогава a.f(p) = a²(p - x₁)(p - x₂) < 0.
достатъчност:
т а.f(p) < 0 следва, че р (x₁,x₂).
Верността на това твърдение е очевидна и следва непосредствено от двете помощни задачи.

Пример 1:
За кои стойности на параметъра "k" уравнението 2x² + (2k - 1)x + k - 1 = 0 има два реални и различни корени такива, че числото ½ да е между тях.
a) dза да бъдат корените реални и различни трябва дискриминанатата да бъде положителна. Това се дава от условието k ≠ 3/2;
б) като приложим доказаното твърдение, т.е. 2.f(½) < 0, получаваме условието k < ½.
Следователно от (а) и от (б) стигаме до извода, че всички стойности на параметъра k, удовлетворяващи изискванията в задачата, са числата по-малки от ½.
За формулитрането на следващото необходимо и достатъчно условие е необходимо да се решат нови помощни задачи.

5. За кои стойности на параметъра р уравнението x² - 7x + p + 5 = 0 има реални корени и точно един е между чилсата 1 и 3.
За решаване на задачата се преминава през същите етапи, както при задача 3.
а) D > 0 дава условие за р.
б) Графиката на функцията така, както на фигура 4.
в) От графиката се вижда, че ако x₂ е между чилста 1 и 3, то f(1) > 0; f(3) < 0 => f(1).f(3) < 0. Същото важи и ако х е между числата 1 и 3.

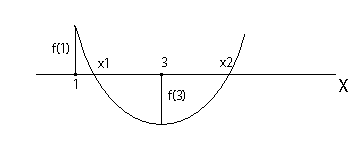
Условието f(1).f(3) < 0 дава окончателно 1 < k < 7.

6. За кои отрицателни стойности на параметъра точно единият от корените на уравнението kx² + 5x + 2 = 0 е между числата -1 и 1.
а) D > 0 ( k < 25/8)
б) Отново графиката на фигура 5.
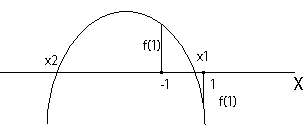
в) От графиката се вижда, че е в сила същото условие:
f(-1).f(1) < 0.

Може да се обощо - независимо от знака на коефициента пред втората степен на квадратното уравнение, условието точно един от корените му да принадлежи на интервала (m,n) е: f(m).f(n) < 0. Това твърдениве е също необходимо и достатъчно условие. Доказателството не е необходимо.
Формулира се и се решава втора задача - компонент на дадената.
За кои стойности на k уравнението 2x² + (2k - 1)x + k - 1 = 0 точно един от корените му е между -1 и 0.
Необходимото и достатъчно условие и двете помощни задачи помагат за решаване на тази задача. Получава се k < ½.
Решаването на двете задачи-компоненти в същност дава решението на дадената задача. Предимството на този подход е в това, че успоредно с решаването на всички задачи се овладяват методи, които могат да се използват при решаване на сложни задачи от този вид.

Задачи

1. За кои сътойности на k уравнението (1 + k)x² - 3kx + 4k = 0 има реални корени по-големи от числото -1?

2. За кои стойности на p уравнението 2x² - 4(p + 2)x + p² + 1 = 0 има реални корени по-малки от 0,5?

3. Дадено е квадратно уравнение 4kx² + 8(1 - k)x + 3k - 13 = 0. За кои стойности на k числото 1 е между x₁ и x₂?

4. а кои стойности на р корените x₁ и x₂ на уравнението 2x² - (2p - 5)x + p - 3 = 0 са между 0 и 1?

5. Да се намерят стойноститена м, така че единият от корените на квадратното уравнение mx² + (7m + 4)x - 4 = 0 да е между 1 и 2, а другият да бъде по-голям от 2?