|
Логаритъм
|

|
|
Алгоритъм Алгоритъм за пресмятане на logb(x), ако b и x са рационални числа и Инициализация Ако n0 е най-голямото естествено число, такова че 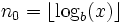 тогава, Стъпка 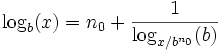 Формула Ако съпката се приложи рекурсивно, се получава безкрайната дроб: 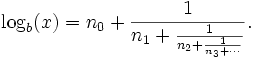 На фиг. 1 можете да видите първите 2 приближения пресметнати по този алгоритъм, т.е. Фиг. 1
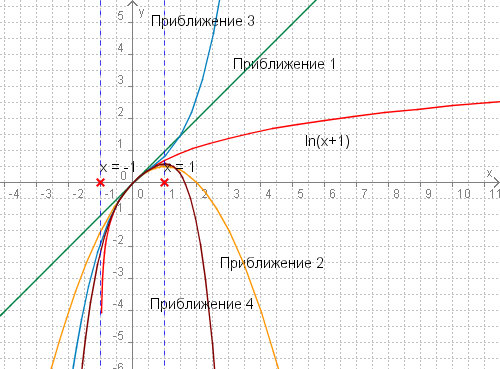
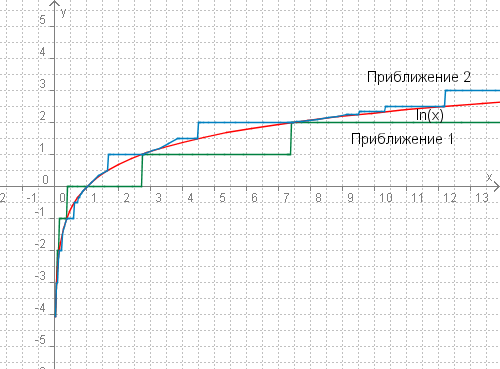 Пресметнатите по-този алгоритъм логаритми, в повечето случаи са ирационални числа Разлагане в ред на Тейлър ln(1 + x) = x - x2/2 + x3/3 - xn/n + ... , където n = 1, 2, 3, ... Това е ралагането на ln() в ред на Тейлър, около точката x = 1. Този ред е верен, само когато |x| < 1, т.е. с този ред могат да се смятат само логаритми в интервала (0, 2). На фиг. 2 можете да видите първите 4 приближения на този ред, т.е. ƒn(x) за Фиг. 2
 |
Доказателство
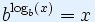 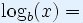 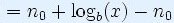 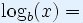 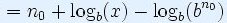 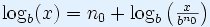 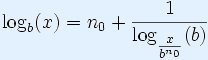 |

 Меню
Меню
